3.3. 演習:網膜疾患診断#
光干渉断層撮影(optical coherence tomography; OCT)は眼底検査に利用され、加齢黄斑変性や糖尿病網膜症などの疾患の早期発見や経過観察に役立っています。本節では、光干渉断層撮影画像を使用し、物体分類のための深層ニューラルネットワークアーキテクチャである ResNet を活用して、網膜疾患を判定するモデルの構築方法を学びます。
3.3.1. 演習準備#
3.3.1.1. ライブラリ#
本節で利用するライブラリを読み込みます。NumPy、Pnadas、Matplotlib、Pillow(PIL)などのライブライは、モデルの性能や推論結果などの可視化に利用します。scikit-learn(sklearn)、PyTorch(torch)、torchvision は機械学習関連のライブラリであり、モデルの構築、検証や推論などに利用します。また、OpenCV(cv2)、pytorch_grad_cam(grad-cam)などはモデルの推論根拠を可視化するために利用します。
# image
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import PIL.Image
# machine learning
import sklearn.metrics
import torch
import torchvision
# grad-CAM visualization
import cv2
import pytorch_grad_cam
print(f'torch v{torch.__version__}; torchvision v{torchvision.__version__}')
torch v2.8.0+cu126; torchvision v0.23.0+cu126
ライブラリの読み込み時に ImportError や ModuleNotFoundError が発生した場合は、該当するライブラリをインストールしてください。ライブラリのバージョンを揃える必要はありませんが、PyTorch(torch)および torchvision が上記のバージョンと異なる時、実行中に警告メッセージが現れたり、同じ結果にならなかったりする可能性があります。
3.3.1.2. データセット#
本節では OCT2017[1] を使用します。このデータセットは、光干渉断層撮影(optical coherence tomography; OCT)で撮影された網膜の画像を、健康(NORMAL)、加齢黄斑変性による脈絡膜新生血管(choroidal neovascularization; CNV)、糖尿病黄斑浮腫(diabetic macular edema; DME)、および網膜色素上皮の機能低下により生じるドルーゼン(DRUSEN)の 4 つのカテゴリに整理されています(Fig. 3.11)。
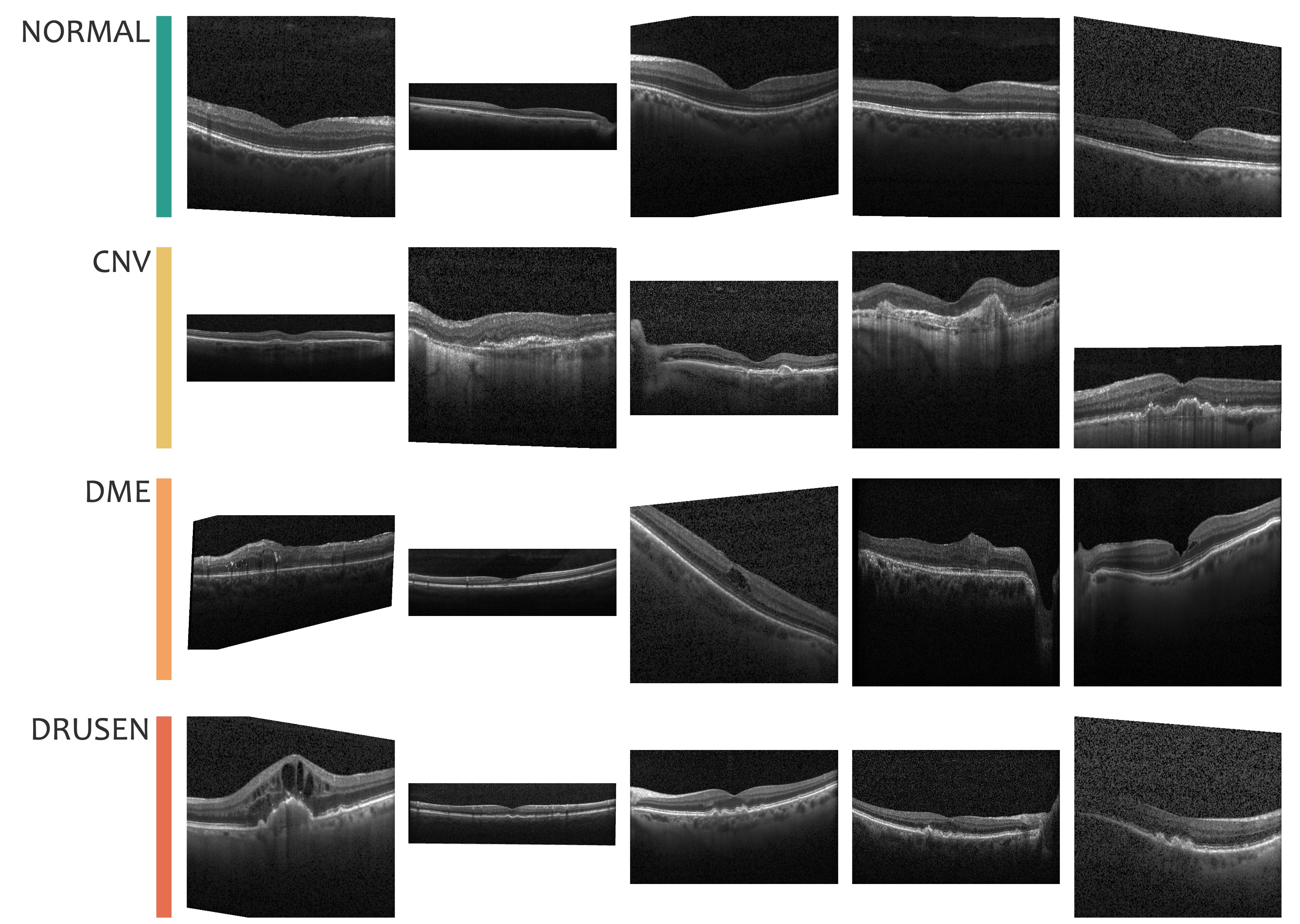
Fig. 3.11 OCT2017 データセットに含まれる各カテゴリのサンプル画像。#
OCT2017 データセットは、CC-BY 4.0 ライセンスのもと、Mendeley Data で公開されており、著作権表示を行うことで自由に利用できます。オリジナルデータセットは大きいため、本節では、オリジナルのデータセットから 1,200 枚の画像をランダムに抽出して作成した小規模なデータセットを使用します。本節で利用するデータセットは、Jupyter Notebook 上では、次のコマンドを実行することでダウンロードできます。
!wget https://dl.biopapyrus.jp/data/oct2017.zip
!unzip oct2017.zip
このデータセットは、訓練、検証、およびテストの 3 つのサブセットで構成されています。訓練サブセットには各カテゴリに 200 枚の画像が含まれています。また、検証およびテストサブセットには、それぞれ各カテゴリごとに 50 枚の画像が含まれています。
3.3.1.3. 画像前処理#
畳み込みニューラルネットワークは、ニューロンの数などが固定されているため、入力する画像のサイズにも制限があります。例えば、本節で使用する ResNet 18 [2] では、224×224 ピクセルの正方形画像を入力として設計されています。また、PyTorch ではすべてのデータをテンソル形式で扱う必要があります。そのため、畳み込みニューラルネットワークに画像を入力する前に、画像サイズを適切に調整し、テンソル型に変換するといった前処理を行う必要があります。以下では、この前処理の手順を定義します。
class SquareResize:
def __init__(self, shape=224, bg_color = (0, 0, 0)):
self.shape = shape
self.bg_color = tuple(bg_color)
def __call__(self, img):
w, h = img.size
img_square = None
if w == h:
img_square = img
elif w > h:
img_square = PIL.Image.new(img.mode, (w, w), self.bg_color)
img_square.paste(img, (0, (w - h) // 2))
else:
img_square = PIL.Image.new(img.mode, (h, h), self.bg_color)
img_square.paste(img, ((h - w) // 2, 0))
img_square = img_square.resize((self.shape, self.shape))
return img_square
transform = torchvision.transforms.Compose([
SquareResize(),
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
画像データは通常、0 から 255 の範囲の整数値で表現されていますが、前処理の段階でこれを正規化します。正規化により、画像データの値は平均約 0.5、標準偏差約 0.23 の範囲に変換され、モデルの学習を効率的に進めることができます。なお、正規化の際に平均を 0.50、分散を 0.23 のような切りの良い数値にしない理由は、これから利用する torchvision.models が提供する訓練済みモデルが、特定の数値(例えば平均 0.485、標準偏差 0.229)で訓練されているためです。そのため、この訓練済みモデルに合わせて正規化を行います。
3.3.1.4. 計算デバイス#
計算を実行するデバイスを設定します。PyTorch が GPU を認識できる場合は GPU を使用し、認識できない場合は CPU を利用するようにします。Google Colab を利用している場合は、メニューから「Runtime」→「Change runtime type」を選び、「Hardware accelerator」を GPU(例: T4 GPU や A100 GPU など)に設定することで、GPU を利用できるようになります。なお、ランタイムを変更すると、Google Colab が再起動されるので、上のコードをもう一度実行する必要があります。
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
3.3.2. モデル構築#
torchvision.models モジュールで提供されているアーキテクチャは、飛行機や車、人など、1000 種類の一般的な物体を分類するように設計されています。これに対して、本節では、NORMAL、CNV、DME および DRUSEN の 4 カテゴリの分類問題を扱います。そのため、torchvision.models モジュールから読み込んだ ResNet 18 の出力層のユニット数を 4 に変更する必要があります。この修正作業はモデルを呼び出すたびに行う必要があり、手間がかかります。そこで、一連の処理を関数化してから利用します。
def resnet18(num_classes, weights=None):
model = torchvision.models.resnet18(weights='DEFAULT')
in_features = model.fc.in_features
model.fc = torch.nn.Linear(in_features, num_classes)
if weights is not None:
model.load_state_dict(torch.load(weights))
return model
model = resnet18(4)
3.3.3. モデル訓練#
モデルが学習データを効率よく学習できるようにするため、損失関数(criterion)、学習アルゴリズム(optimizer)、学習率(lr)、および学習率を調整するスケジューラ(lr_scheduler)を設定します。
optimizer = torch.optim.Adam(model.parameters(), lr=0.0001)
criterion = torch.nn.CrossEntropyLoss()
lr_scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=3, gamma=0.1)
次に、訓練データと検証データを読み込み、モデルが入力できる形式に整えます。
train_dataset = torchvision.datasets.ImageFolder('oct2017/train', transform=transform)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=32, shuffle=True)
valid_dataset = torchvision.datasets.ImageFolder('oct2017/valid', transform=transform)
valid_loader = torch.utils.data.DataLoader(valid_dataset, batch_size=32, shuffle=False)
準備が整ったら、訓練を開始します。訓練プロセスでは、訓練と検証を交互に繰り返します。訓練では、訓練データを使ってモデルのパラメータを更新し、その際の損失(誤差)を記録します。検証では、検証データを使ってモデルの予測性能(正解率)を計算し、その結果を記録します。
model.to(device)
num_epochs = 10
metric_dict = []
for epoch in range(num_epochs):
# training phase
model.train()
running_loss = 0.0
n_correct_train = 0
n_train_samples = 0
for images, labels in train_loader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
loss = criterion(outputs, labels)
_, predicted_labels = torch.max(outputs.data, 1)
n_correct_train += torch.sum(predicted_labels == labels).item()
n_train_samples += labels.size(0)
running_loss += loss.item() / len(train_loader)
optimizer.zero_grad()
loss.backward()
optimizer.step()
lr_scheduler.step()
# validation phase
model.eval()
n_correct_valid = 0
n_valid_samples = 0
with torch.no_grad():
for images, labels in valid_loader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
_, predicted_labels = torch.max(outputs.data, 1)
n_correct_valid += torch.sum(predicted_labels == labels).item()
n_valid_samples += labels.size(0)
metric_dict.append({
'epoch': epoch + 1,
'train_loss': running_loss,
'train_acc': n_correct_train / n_train_samples,
'valid_acc': n_correct_valid / n_valid_samples
})
print(metric_dict[-1])
Show code cell output
{'epoch': 1, 'train_loss': 0.8395686411857607, 'train_acc': 0.65125, 'valid_acc': 0.645}
{'epoch': 2, 'train_loss': 0.2518396836519241, 'train_acc': 0.91125, 'valid_acc': 0.755}
{'epoch': 3, 'train_loss': 0.09454739421606065, 'train_acc': 0.97875, 'valid_acc': 0.83}
{'epoch': 4, 'train_loss': 0.029935829527676105, 'train_acc': 1.0, 'valid_acc': 0.825}
{'epoch': 5, 'train_loss': 0.027070958018302914, 'train_acc': 0.99875, 'valid_acc': 0.825}
{'epoch': 6, 'train_loss': 0.02702774304896593, 'train_acc': 0.9975, 'valid_acc': 0.83}
{'epoch': 7, 'train_loss': 0.022205655165016654, 'train_acc': 1.0, 'valid_acc': 0.83}
{'epoch': 8, 'train_loss': 0.02144889988005162, 'train_acc': 1.0, 'valid_acc': 0.82}
{'epoch': 9, 'train_loss': 0.018948247991502284, 'train_acc': 1.0, 'valid_acc': 0.83}
{'epoch': 10, 'train_loss': 0.026732975821942086, 'train_acc': 0.99875, 'valid_acc': 0.83}
訓練データに対する損失と検証データに対する正解率を可視化し、訓練過程を評価します。
Show code cell source
metric_dict = pd.DataFrame(metric_dict)
fig, ax = plt.subplots(1, 2)
ax[0].plot(metric_dict['epoch'], metric_dict['train_loss'])
ax[0].set_xlabel('epoch')
ax[0].set_ylabel('loss')
ax[0].set_title('Train')
ax[1].plot(metric_dict['epoch'], metric_dict['valid_acc'])
ax[1].set_ylim(0, 1)
ax[1].set_xlabel('epoch')
ax[1].set_ylabel('accuracy')
ax[1].set_title('Validation')
plt.tight_layout()
fig.show()

訓練過程を可視化した結果、エポックが進むにつれて訓練データに対する損失が減少し、5 エポック前後で収束し始める傾向が確認できました。また、検証データに対する分類性能(正解率)は、最初の数エポックで既に高い性能を示していることがわかりました。
次に、同じ手順を他の深層ニューラルネットワークアーキテクチャ(DenseNet や Inception など)に対して実施し、それぞれの検証性能を比較します。そして、このデータセットに最適なアーキテクチャを選定します。ただし、本節ではモデル(アーキテクチャ)選択を行わずに、ResNet 18 を最適なアーキテクチャとして採用し、次のステップに進みます。
次のステップでは、訓練サブセットと検証サブセットを統合し、最適なアーキテクチャで最初から訓練を行います。
!mkdir oct2017/trainvalid
!cp -r oct2017/train/* oct2017/trainvalid
!cp -r oct2017/valid/* oct2017/trainvalid
最適なモデルを選択する段階で、数エポックの訓練だけでも十分に高い予測性能を獲得できたことがわかったので、ここでは訓練サブセットと検証サブセットを統合したデータに対して 5 エポックだけ訓練させます。
# model
model = resnet18(4)
model.to(device)
# training params
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.0001)
lr_scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=3, gamma=0.1)
# training data
train_dataset = torchvision.datasets.ImageFolder('oct2017/trainvalid', transform=transform)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=32, shuffle=True)
# training
num_epochs = 5
metric_dict = []
for epoch in range(num_epochs):
model.train()
running_loss = 0.0
n_correct_train = 0
n_train_samples = 0
for images, labels in train_loader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
loss = criterion(outputs, labels)
_, predicted_labels = torch.max(outputs.data, 1)
n_correct_train += torch.sum(predicted_labels == labels).item()
n_train_samples += labels.size(0)
running_loss += loss.item() / len(train_loader)
optimizer.zero_grad()
loss.backward()
optimizer.step()
lr_scheduler.step()
metric_dict.append({
'epoch': epoch + 1,
'train_loss': running_loss,
'train_acc': n_correct_train / n_train_samples,
})
print(metric_dict[-1])
Show code cell output
{'epoch': 1, 'train_loss': 0.7696597287431359, 'train_acc': 0.691}
{'epoch': 2, 'train_loss': 0.23688622517511249, 'train_acc': 0.914}
{'epoch': 3, 'train_loss': 0.09686957945814356, 'train_acc': 0.974}
{'epoch': 4, 'train_loss': 0.04559963056817651, 'train_acc': 0.992}
{'epoch': 5, 'train_loss': 0.029219637042842805, 'train_acc': 0.996}
訓練が完了したら、訓練済みモデルの重みをファイルに保存します。
model = model.to('cpu')
torch.save(model.state_dict(), 'oct2017.pth')
3.3.4. モデル評価#
最適なモデルが得られたら、次にテストデータを用いてモデルを詳細に評価します。正解率だけでなく、適合率、再現率、F1 スコアなどの評価指標を計算し、モデルを総合的に評価します。まず、テストデータをモデルに入力し、その予測結果を取得します。
model = resnet18(4, 'oct2017.pth')
model.to(device)
model.eval()
test_dataset = torchvision.datasets.ImageFolder('oct2017/test', transform=transform)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=32, shuffle=False)
pred_labels = []
true_labels = []
with torch.no_grad():
for images, labels in test_loader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
_, _labels = torch.max(outputs.data, 1)
#print(_labels)
pred_labels.extend(_labels.cpu().detach().numpy().tolist())
true_labels.extend(labels.cpu().detach().numpy().tolist())
pred_labels = [test_dataset.classes[_] for _ in pred_labels]
true_labels = [test_dataset.classes[_] for _ in true_labels]
次に、予測結果とラベルを比較し、混同行列を作成します。これにより、間違いやすいカテゴリを特定することができます。
cm = sklearn.metrics.confusion_matrix(true_labels, pred_labels)
cm
array([[46, 3, 1, 0],
[ 2, 47, 1, 0],
[ 1, 0, 49, 0],
[ 0, 0, 2, 48]])
cmp = sklearn.metrics.ConfusionMatrixDisplay(cm, display_labels=test_dataset.classes)
cmp.plot()
<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x7f681046a250>

それぞれのクラスに対する適合率、再現率、F1 スコアなどは、scikit-learn ライブラリを利用して計算します。
pd.DataFrame(sklearn.metrics.classification_report(true_labels, pred_labels, output_dict=True))
| CNV | DME | DRUSEN | NORMAL | accuracy | macro avg | weighted avg | |
|---|---|---|---|---|---|---|---|
| precision | 0.938776 | 0.94 | 0.924528 | 1.000000 | 0.95 | 0.950826 | 0.950826 |
| recall | 0.920000 | 0.94 | 0.980000 | 0.960000 | 0.95 | 0.950000 | 0.950000 |
| f1-score | 0.929293 | 0.94 | 0.951456 | 0.979592 | 0.95 | 0.950085 | 0.950085 |
| support | 50.000000 | 50.00 | 50.000000 | 50.000000 | 0.95 | 200.000000 | 200.000000 |
3.3.5. 推論#
推論を行う際には、訓練や評価時と同様に、torchvision.models モジュールから ResNet 18 のアーキテクチャを読み込み、出力層のクラス数を設定します。その後、load_state_dict メソッドを使用して訓練済みの重みファイルをモデルにロードします。これらの処理はすでに関数化(resnet18)されているため、その関数を利用して簡単に実行できます。
labels = ['CNV', 'DME', 'DRUSEN', 'NORMAL']
model = resnet18(4, 'oct2017.pth')
model.to(device)
model.eval()
Show code cell output
ResNet(
(conv1): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
(layer1): Sequential(
(0): BasicBlock(
(conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(1): BasicBlock(
(conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(layer2): Sequential(
(0): BasicBlock(
(conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(downsample): Sequential(
(0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(layer3): Sequential(
(0): BasicBlock(
(conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(downsample): Sequential(
(0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(layer4): Sequential(
(0): BasicBlock(
(conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(downsample): Sequential(
(0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(avgpool): AdaptiveAvgPool2d(output_size=(1, 1))
(fc): Linear(in_features=512, out_features=4, bias=True)
)
このモデルを使って推論を行います。まず、polyps の画像を 1 枚選び、訓練時と同じ前処理を施します。その後、前処理をした画像をモデルに入力し、予測結果を表示させます。
image_path = 'oct2017/test/CNV/CNV-198660-1.jpeg'
image = PIL.Image.open(image_path).convert('RGB')
input_tensor = transform(image).unsqueeze(0).to(device)
with torch.no_grad():
score = model(input_tensor)[0]
output = pd.DataFrame({
'class': labels,
'probability': torch.softmax(score, axis=0).cpu().detach().numpy()
})
output
| class | probability | |
|---|---|---|
| 0 | CNV | 0.998567 |
| 1 | DME | 0.000166 |
| 2 | DRUSEN | 0.001126 |
| 3 | NORMAL | 0.000141 |
もう一例を見てみましょう。DME の画像をモデルに入力し、推論を行います。
image_path = 'oct2017/test/DME/DME-269181-1.jpeg'
image = PIL.Image.open(image_path).convert('RGB')
input_tensor = transform(image).unsqueeze(0).to(device)
with torch.no_grad():
score = model(input_tensor)[0]
pd.DataFrame({
'class': labels,
'probability': torch.softmax(score, axis=0).cpu().detach().numpy()
})
| class | probability | |
|---|---|---|
| 0 | CNV | 0.028769 |
| 1 | DME | 0.948855 |
| 2 | DRUSEN | 0.018312 |
| 3 | NORMAL | 0.004064 |
3.3.6. 分類根拠の可視化#
畳み込みニューラルネットワークを用いた画像分類では、畳み込み層で抽出された特徴マップが分類に大きな影響を与えています。そのため、最後の畳み込み層で得られた特徴マップと、それに対応する重みを可視化することで、モデルがどの部分に注目して分類を行ったのか、つまり判断の根拠を明確にすることができます。
本節では、Grad-CAM(Gradient-weighted Class Activation Mapping)および Guided Grad-CAM という手法を用いて、モデルの判断根拠を可視化します。可視化には Python の grad-cam パッケージを使用します。必要に応じてインストールし、grad-cam のチュートリアルを参考にしながら、Grad-CAM および Guided Grad-CAM を計算し、可視化するための関数を定義します。
def viz(image_path):
# load models
labels = ['CNV', 'DME', 'DRUSEN', 'NORMAL']
model = resnet18(4, 'oct2017.pth')
model.to(device)
model.eval()
# load image
image = PIL.Image.open(image_path).convert('RGB')
input_tensor = transform(image).unsqueeze(0).to(device)
rgb_img = cv2.imread(image_path, 1)[:, :, ::-1]
rgb_img = np.float32(np.array(SquareResize()(image))) / 255
# Grad-CAM
with pytorch_grad_cam.GradCAM(model=model, target_layers=[model.layer4]) as cam:
cam.batch_size = 32
grayscale_cam = cam(input_tensor=input_tensor, targets=None,aug_smooth=True, eigen_smooth=True)
grayscale_cam = grayscale_cam[0, :]
cam_image = pytorch_grad_cam.utils.image.show_cam_on_image(rgb_img, grayscale_cam, use_rgb=True)
prob = torch.softmax(cam.outputs[0], axis=0).cpu().detach().numpy()
gb_model = pytorch_grad_cam.GuidedBackpropReLUModel(model=model, device=device)
gb = gb_model(input_tensor, target_category=None)
cam_mask = np.stack([grayscale_cam, grayscale_cam, grayscale_cam], axis=-1)
cam_gb = pytorch_grad_cam.utils.image.deprocess_image(cam_mask * gb)
gb = pytorch_grad_cam.utils.image.deprocess_image(gb)
# plot
fig, ax = plt.subplots(2, 2)
ax[0, 0].imshow(rgb_img)
ax[0, 0].axis('off')
ax[0, 0].set_title('Original Image', fontsize=16)
ax[0, 1].imshow(cam_image)
ax[0, 1].axis('off')
ax[0, 1].set_title('Grad-CAM', fontsize=16)
ax[1, 0].imshow(gb)
ax[1, 0].axis('off')
ax[1, 0].set_title('Guided Backpropagation', fontsize=16)
ax[1, 1].imshow(cam_gb)
ax[1, 1].axis('off')
ax[1, 1].set_title('Guided Grad-CAM', fontsize=16)
print(pd.DataFrame({'class': labels, 'probability': prob}))
fig.show()
次に、いくつかの画像をこの可視化関数に入力し、モデルの予測結果とその判断根拠を可視化します。これにより、モデルがどの部分に注目して分類を行ったのかを視覚的に確認することができます。必要に応じて、他の画像を入力し、それぞれの分類結果と判断根拠を可視化してみてください。
viz('oct2017/test/CNV/CNV-198660-1.jpeg')
class probability
0 CNV 0.963380
1 DME 0.001755
2 DRUSEN 0.033909
3 NORMAL 0.000956

viz('oct2017/test/DME/DME-269181-1.jpeg')
class probability
0 CNV 0.005694
1 DME 0.977940
2 DRUSEN 0.013577
3 NORMAL 0.002790

viz('oct2017/test/DRUSEN/DRUSEN-1730592-1.jpeg')
class probability
0 CNV 0.015999
1 DME 0.000439
2 DRUSEN 0.983100
3 NORMAL 0.000462

viz('oct2017/test/NORMAL/NORMAL-402066-5.jpeg')
class probability
0 CNV 0.000210
1 DME 0.000296
2 DRUSEN 0.001672
3 NORMAL 0.997822


