2.6. ゲート付き再帰ユニット#
ゲート付き再帰ユニット(gated recurrent unit; GRU)は、長期依存性を学習する能力を持つ再帰型ニューラルネットワークの一種です。GRU は、RNN における勾配消失問題を緩和し、長期依存関係を効果的に学習できるアーキテクチャです。
GRU は、LSTM と同様に、長期依存性を扱うことができますが、LSTM に比べてモデルがシンプルで計算量が少ないという利点があります。GRU は、LSTM のセルにおける複雑な構造を省略し、2 つのゲート(リセットゲートとアップデートゲート)だけで情報の保持と更新を行います。このため、訓練が速く、より効率的に学習できます。また、LSTM より少ないパラメータで同様の性能を発揮することが多いため、リソースの限られた環境でも活用できます。
2.6.1. アーキテクチャ#
GRU は、通常の RNN と同様に、データが入力層、中間層、出力層を通じて伝播されます。しかし、RNN の中間層は活性化関数が 1 つだけであるのに対して、GRU の中間層には複数の活性化関数が用意され、ゲートを使って情報の流れを制御します。このゲートの仕組みによって、GRU は必要な情報を選択的に保持し、不必要な情報を忘れることができます。
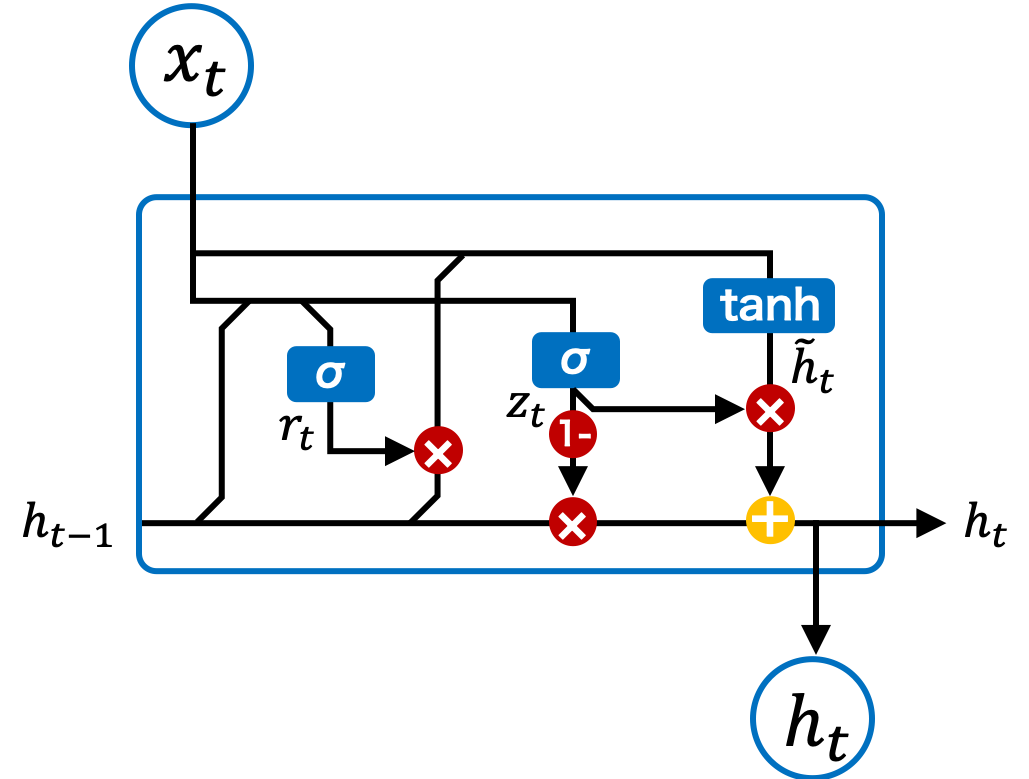
Fig. 2.9 GRU ブロックのアーキテクチャ。#
2.6.2. リセットゲート#
リセットゲート(reset gate)は、GRU の中で過去の情報をどれだけ忘れるかを制御します。具体的には、現在の入力情報 \(\mathbf{x}_{t}\) と一つ前の隠れ状態 \(\mathbf{h}_{t-1}\) を使って、リセットゲートの値 \(\mathbf{r}_{t}\) を計算します。リセットゲートの値によって、どの程度前の隠れ状態を「忘れるか」が決まります。リセットゲートはシグモイド関数で計算され、値は 0 から 1 の範囲になります。
このリセットゲートで計算される値 \(\mathbf{r}_{t}\) は、前の状態の隠れ状態 \(\mathbf{h}_{t-1}\) にかけられ、どの程度その情報を保持するか、または忘れるかを制御します。LSTM の忘却ゲートと似た役割を果たします。
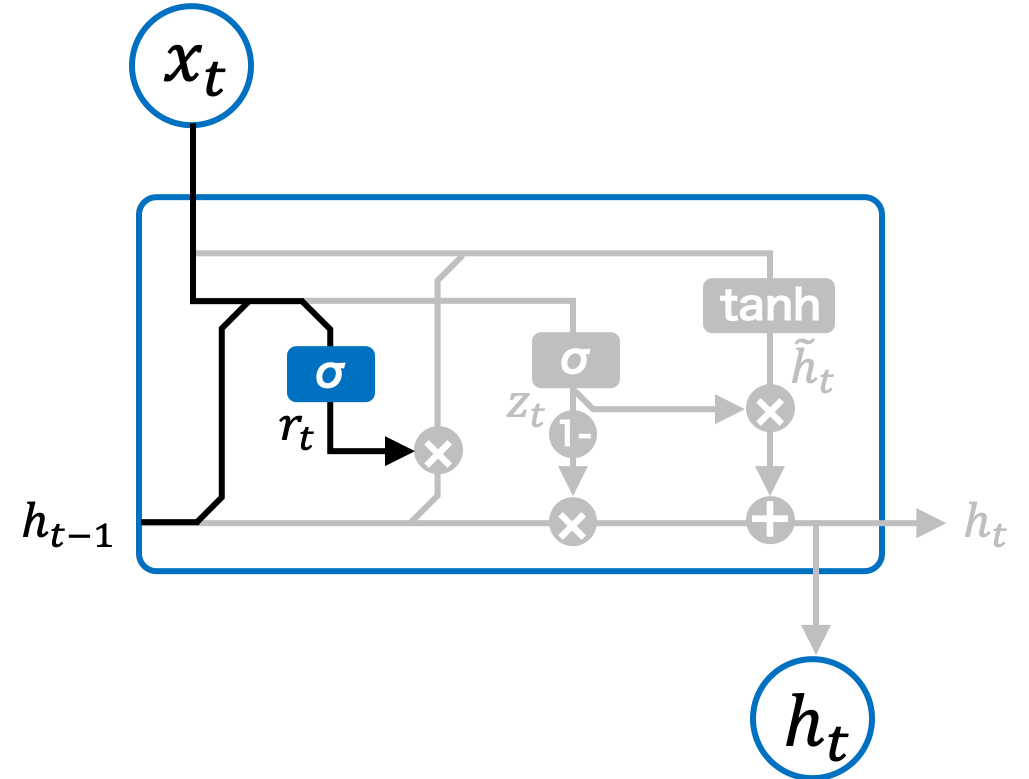
Fig. 2.10 GRU ブロックのリセットゲート。#
2.6.3. アップデートゲート#
アップデートゲート(update gate)は、過去の状態から伝達された長期記憶 \(\mathbf{h}_{t-1}\) と、現在の状態から計算された新しい情報 \(\tilde{\mathbf{h}}_{t}\) を、ある割合で混ぜ合わせる役割を持ちます。このゲートによって、どの程度新しい情報を取り入れるか、どの程度前の状態を保持するかが決まります。
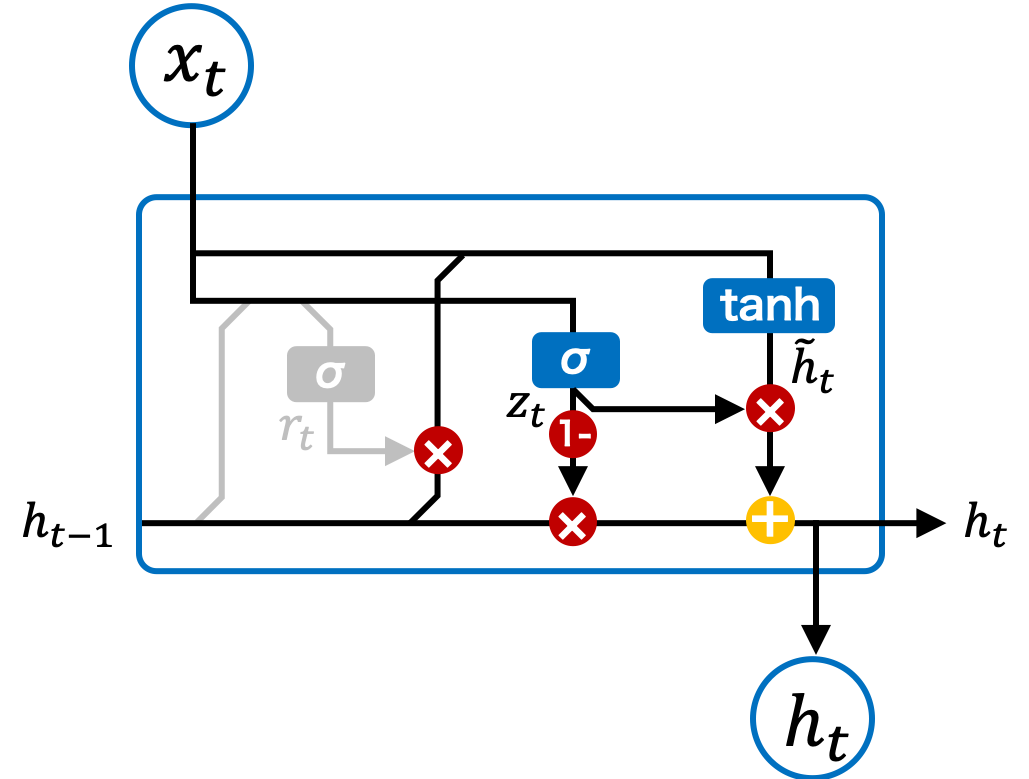
Fig. 2.11 GRU ブロックのアップデートゲート。#
最初に、リセットゲートを使って計算された新しい状態 \(\tilde{\mathbf{h}}_{t}\) は以下のように求められます。
次に、アップデートゲート \(\mathbf{z}_{t}\) を計算します。アップデートゲートは、現在の状態と前の状態をどれくらいの割合で混合するかを制御します。アップデートゲートは、入力 \(\mathbf{x}_{t}\) と前の隠れ状態 \(\mathbf{h}_{t-1}\) を基に計算され、シグモイド関数を使用してそれを 0 から 1 の間の値に変換します。
最後に、長期記憶は以下のように更新され、次の状態に伝播されます。
この式により、現在の状態と前の状態が適切な割合で混合され、それが新しい状態として出力され、また、次の時刻に引き継がれます。