評価指標 mAP

4.2. 評価指標 mAP#

物体検出モデルの性能を評価する指標のひとつに mAP (mean Average Precision) があります。mAP は、モデルがどれだけ正確に物体を検出できるかを示す値で、一般に 0 から 1 の範囲をとり、1 に近いほど検出性能が高いことを意味します。

4.2.1. AP (Average Precision)#

mAP の計算の基本となるのが AP (Average Precision; 平均適合率) です。AP は、特定のクラスに対するモデルの検出性能を測る指標です。データセットに複数のクラス（例えば腫瘍性ポリープや炎症性ポリープなど）が含まれている場合、それぞれのクラスに対して AP を計算する必要があります。

ここでは、腫瘍性ポリープに対する AP の計算方法の具体例を見ていきます。計算が簡単となるようにシンプルな事例を考えます。モデルの検証に使った画像を 20 枚であったとします。これらの画像において、1 枚の画像の中に複数の腫瘍性ポリープが含まれる場合もあれば、まったく含まれない場合もあります。すべての画像を集計すると、合計 5 個の腫瘍性ポリープが存在していたとします。また、今回は、腫瘍性ポリープの検出性能を評価することが目的であるため、データセット内に炎症性ポリープなど他のラベルが含まれていても、それらは考慮しません。

AP を計算するためには、適合率（Precision）、再現率（Recall）、および IoU（Intersection over Union）について理解しておく必要があります。これらの指標について詳しく見ていきます。

4.2.1.1. 適合率と再現率#

適合率（precision）は、陽性と予測したサンプルの中で、実際に陽性であった割合のことであり、次のように計算されます。

\[ \text{precision} = \frac{\text{TP}}{\text{TP} + \text{FP}} \]

再現率は、実際に存在する陽性のうち、モデルが正しく予測できた割合のことであり、次のように計算されます。

\[ \text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} \]

4.2.1.2. IoU#

IoU（Intersection over Union）は、2 つの領域がどれくらい重なっているかを測る指標です。物体検出では、モデルが予測した領域と、実際の正解領域がどれほど一致しているかを評価する際に使われます。具体的には、「2 つの領域が重なっている部分の面積」を「両方の領域を合わせた全体の面積」で割った値であり（Fig. 4.8）、次のように計算できます。この IoU は、数学で集合の類似度を測るジャッカード係数（Jaccard index）と同じ計算方法になります。

\[ \mathrm{IoU} = \frac{\text{予測領域} \cap \text{正解領域}}{\text{予測領域} \cup \text{正解領域}} \]

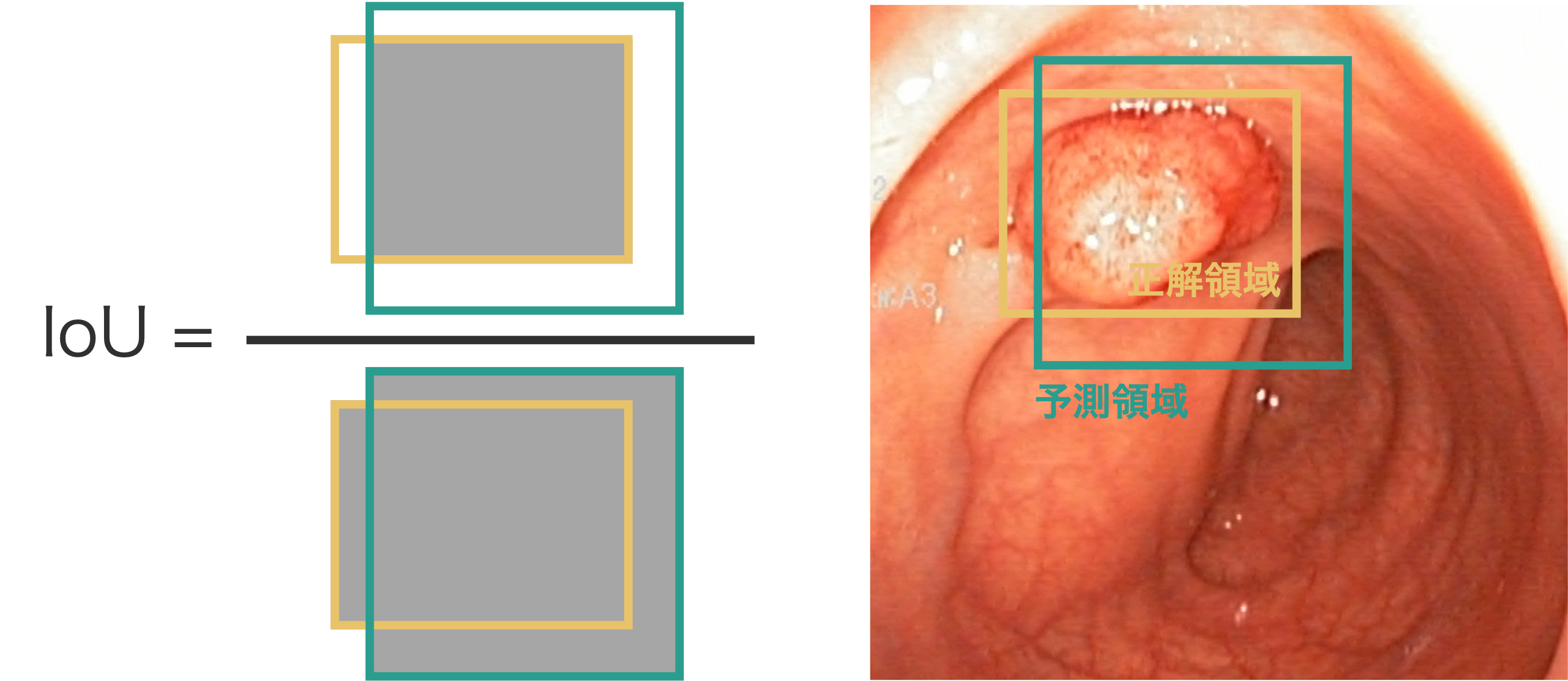
../_images/iou_calc.png — Fig. 4.8 IoU（Intersection over Union）は、予測領域と正解領域が重なっている領域を、予測領域と正解領域の合計領域で割った割合として計算されます。#

例えば、2 つの領域がまったく重なっていなければ IoU は 0 となり、逆に完全に一致していれば IoU は 1 になります。重なりの割合が増えるほど IoU は 1 に近づきます。通常、物体検出では IoU が 0.5 以上であれば、正しく検出できた（true positive）と判断されます。

4.2.1.3. 適合率-再現率曲線#

モデルが物体を検出する際には、予測の確からしさを表す信頼度スコアを出力します。このスコアを降順に並べ、上位の予測結果から順に適合率と再現率を計算し、それを適合率-再現率曲線（PR 曲線）にプロットします。例えば、以下のような予測結果があったとします。

信頼度	IoU ≥ 0.5
0.98	True
0.97	True
0.94	True
0.92	False
0.88	True
0.83	False
0.82	False
0.79	False
0.73	True
0.65	False

次に、これらの 10 個の予測結果に対して、順に適合率と再現率を計算していきます。例えば、1 番目の予測結果に着目すると、この時点までの結果において TP = 1、FP = 0 となります。そのため、適合率は TP/(TP + FP) = 1.0 となります。一方、再現率については、データセット内に腫瘍性ポリープが 5 箇所含まれているにも関わらず、現時点では 1 つしか検出されていないため、再現率は 1/5 = 0.2 となります。

信頼度	IoU ≥ 0.5	適合率	再現率
0.98	True	1.0	0.2

続いて、2 番目の予測結果に着目します。2 行目までの予測がすべて正しいため、適合率は 1.0 となります。一方、再現率については、データセット内の 5 箇所の腫瘍性ポリープのうち 2 箇所を検出できているため、2/5 = 0.4 と計算されます。

信頼度	IoU ≥ 0.5	適合率	再現率
0.98	True	1.0	0.2
0.97	True	1.0	0.4

同様にして、4 番目の予測結果に着目してみます。4 行目までの予測結果を確認すると、4 つの予測のうち 3 つが正しく腫瘍性ポリープを検出できており、1 つが誤検出となっています。そのため、適合率は TP / (TP + FP) = 3 / 4 = 0.75 と計算されます。一方、再現率については、データセット内の 5 箇所のポリープのうち 3 箇所を検出できているため、3 / 5 = 0.6 となります。

信頼度	IoU ≥ 0.5	適合率	再現率
0.98	True	1.0	0.2
0.97	True	1.0	0.4
0.94	True	1.0	0.6
0.92	False	0.75	0.6

このような計算で、すべての予測結果について、適合率と再現率を計算します。

信頼度	IoU ≥ 0.5	適合率	再現率
0.98	True	1.0	0.2
0.97	True	1.0	0.4
0.94	True	1.0	0.6
0.92	False	0.75	0.6
0.88	True	0.8	0.8
0.83	False	0.67	0.8
0.82	False	0.57	0.8
0.79	False	0.5	0.8
0.73	True	0.56	1.0
0.65	False	0.5	1.0

最後に、再現率を横軸に、適合率を縦軸に折れ線グラフを描きます（Fig. 4.9）。このジグザグ状の折れ線グラフを適合率-再現率曲線（PR 曲線）と呼びます。検証データが多くなると、ジグザグ状が目立たなくなり、曲線のように見えます。

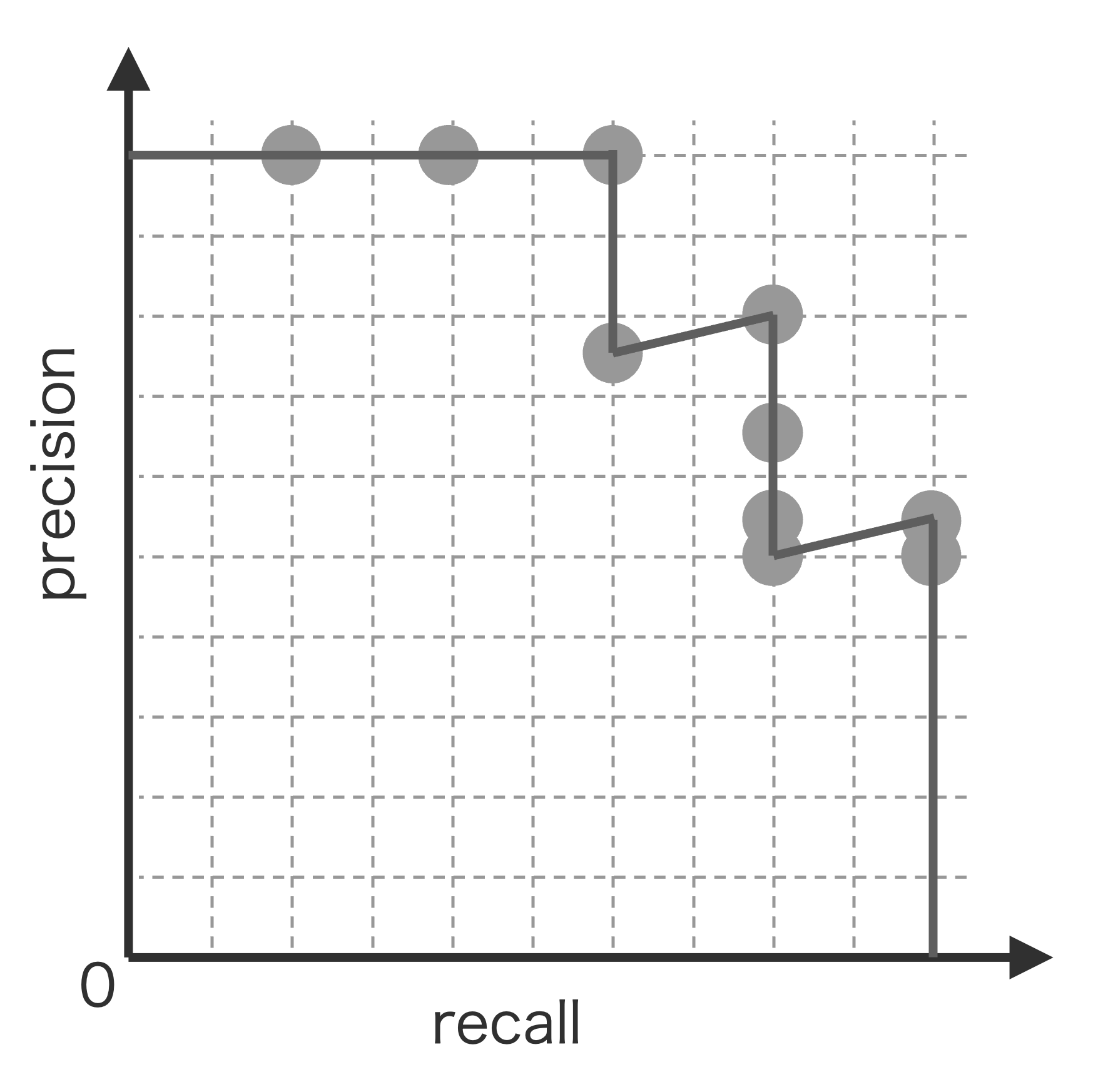
../_images/mAP_pr_curve_01.png — Fig. 4.9 適合率-再現率曲線。#

4.2.1.4. AP の計算#

AP は、適合率-再現率曲線の下の面積として計算されます。ただし、物体検出モデルの性能指標として使用される AP では、まず適合率と再現率の曲線を平坦化し、その後、横軸を 100 等分します。そして、等分割された各座標での適合率の平均を計算して AP を求めます。

具体的に、適合率-再現率曲線の各再現率の値に対し、右側の最大適合率を採用することで平坦化していきます（Fig. 4.10）。

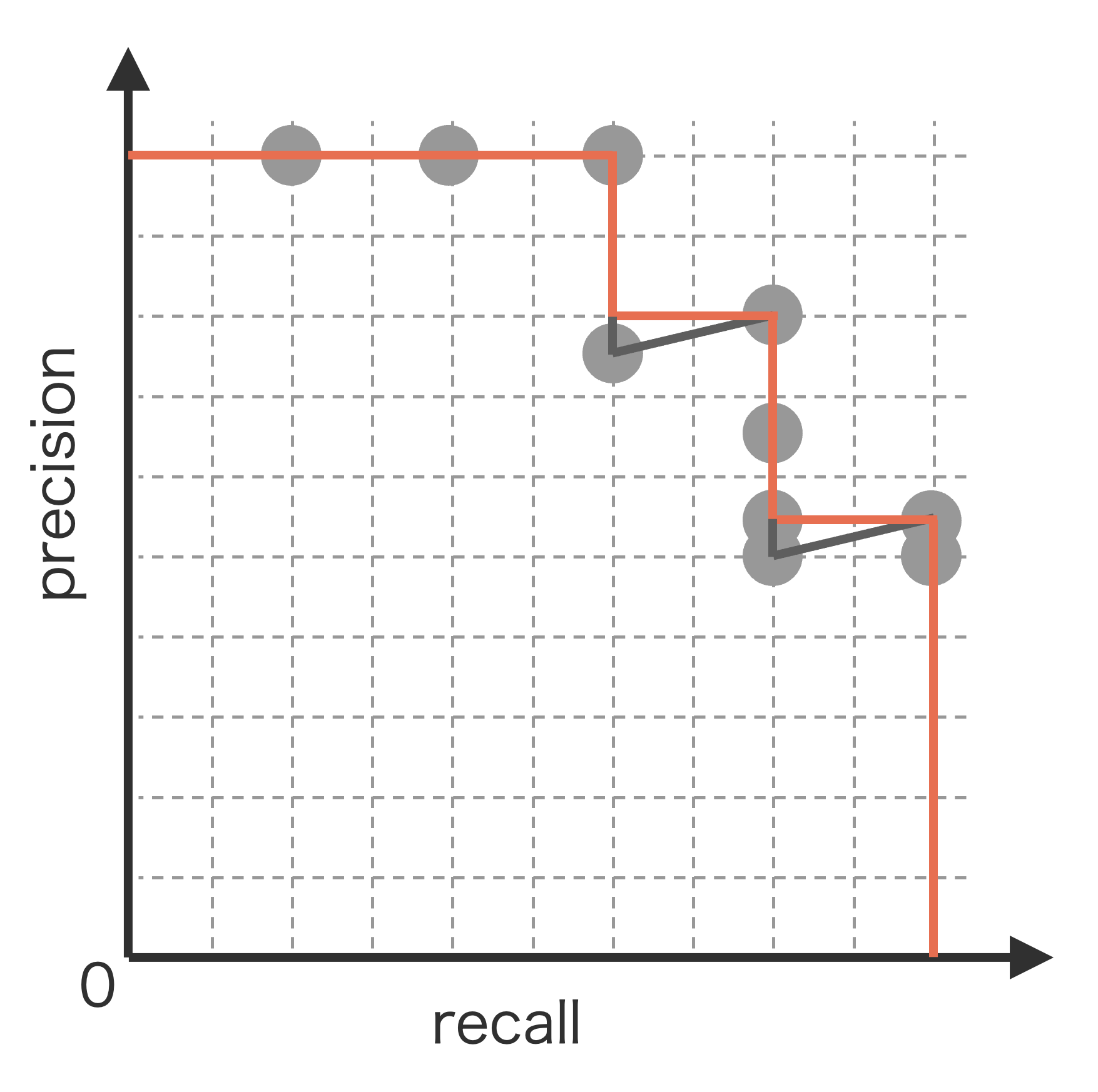
../_images/mAP_pr_curve_02.png — Fig. 4.10 平坦化後の適合率-再現率曲線（赤線）。#

次に、横軸を 100 等分します。100 等分割して得られた座標が 0.0、0.01、・・・、0.99、1.00 となります。横軸の座標 \(r\) に対応する適合率を \(p_r\) とすると、AP は次式で計算されます。

\[ \text{AP} = \frac{1}{101} \sum_{r \in (0.0, 0.01, \dots, 1.0)} p_r \]

この値が、モデルの腫瘍性ポリープの検出性能を評価するための指標 AP となります。

なお、一部の研究では、横軸を 100 等分割するのではなく、10 等分割する方法が採用されています。モデルを使用する際には、該当する研究論文で指標の定義を確認することが重要です。

4.2.2. mAP#

データセットに複数のクラス（例えば、腫瘍性ポリープや炎症性ポリープなど）が含まれている場合、各クラスに対して AP を計算します。そして、それらの AP の平均値が mAP（mean Average Precision）となります。モデルの性能を一つの指標で示す際に、この mAP を使用します。また、この mAP を単に AP と呼ぶこともよくあります。

これまでの説明では、mAP を計算する際に予測領域と正解領域の IoU が 0.5 以上であれば、予測が正しいと見なしました。しかし、実際の研究では、IoU の閾値として 0.5 に加えて 0.75 なども使われることがあります。これらは、mAP₅₀、mAP@[0.5]、mAP₇₅、mAP@[0.75] などのように記載されることが多いです。また、小さなオブジェクト、中程度のオブジェクト、大きなオブジェクトに分けて mAP を計算することもあります。これらは、mAP_S、mAP@[small]、mAP_M、mAP@[medium]、mAP_L、mAP@[large] として表現されます。さらに、IoU を 0.50 から 0.95 まで 0.05 刻みで変更し、その結果得られる mAP を平均した値を用いることもあります。このような mAP は AP@[0.5:0.95] のように表わされます。