1.6. 演習:パーセプトロン#
1.6.1. アルゴリズム#
パーセプトロン(perceptron)は、ニューラルネットワークを構成する基本的なモデルの一つです。このモデルは、入力された特徴量に係数(パラメータ)を掛け合わせ、その合計が 0 以上かどうかを基準にデータを分類する、シンプルなアルゴリズムです。例えば、腫瘍のサイズを特徴量として、その腫瘍細胞が良性か悪性かを予測するケースを考えてみましょう。
パーセプトロンは、ロジスティック回帰と同様に、入力された特徴量に対して係数を掛けて合計値を計算します。ここでこの合計値を \( z \) とします。
次に、この \( z \) が 0 以上であれば「悪性(1)」、0 未満であれば「良性(0)」を出力します。数式で表すと次のようになります。
このとき関数 \(\phi(z)\) のことをステップ関数(step function)と呼びます。ロジスティック回帰では、シグモイド関数を利用して出力値が 0 と 1 の間の値に変換するのに対し、パーセプトロンはステップ関数を用いて出力値を 0 または 1 に変換しています。
また、パーセプトロンのパラメータの推定方法も特徴的です。回帰分析やロジスティック回帰では、すべてのデータを用いて損失を最小化するようにパラメータを推定します。しかし、パーセプトロンでは、まずランダムな値でパラメータを初期化し、以下の更新式に基づいてデータを 1 つずつ処理しながらパラメータを更新していきます。
ここで、モデルの出力値 \(\phi(z) = \phi(\beta_{1}X + \beta_{0})\) と観測値が一致していれば、\((y - \phi(z))\) は 0 となり、\(\beta_{1}\) および \(\beta_{0}\) は更新されません。一方、モデルの出力値と観測値が異なれば、\((y - \phi(z))\) は \(+1\) または \(-1\) となり、新しいパラメータが計算されます。パーセプトロンは同じデータセットをシャッフルしながら何度も学習を繰り返し、パラメータが更新されなくなるまで処理を続けます。このプロセスを学習または適合と呼びます。
\(\eta\) はモデルの出力値と観測値が異なるとき、その誤差をどの程度に拡大あるいは縮小するのかを調整するパラメータです。これを学習率(learning rate)と呼びます。\(\eta\) が大きければ、モデルの出力が間違ったときに、その誤差が拡大され、更新されるパラメータの値は古い値から大きく変化します。逆に、\(\eta\) が小さいと、更新されるパラメータの値は、古い値に近い値となります。最適なパラメータを見つけるためには、この \(\eta\) を適切な値に調節する必要があります。\(\beta_{1}\) や \(\beta_{0}\) はデータから計算(推測)するが、\(\eta\) は人間があらかじめ与えなければなりません。このようなパラメータのことをハイパーパラメータ(hyperprameter)と呼びます。
なお、パーセプトロンは非常にシンプルなモデルであるため、1 本の直線や平面で分離できないようなデータには対応できません。そのような複雑なデータに対しては、複数のパーセプトロンを適切に組み合わせた多層パーセプトロン(MLP)などが用いられます。
1.6.2. 演習準備#
本節では、パーセプトロンの特徴やその限界を説明するために、scikit-learn ライブラリで人工的なサンプルデータを生成して利用します。また、本節では、次の Python ライブラリを利用します。numpy、pandas、matplotlib ライブラリはデータの読み込みや整形、可視化などに利用します。sklearn はサンプルデータセットの生成およびデータセットを訓練サブセットと検証サブセットに分けるために利用します。
import numpy as np
import pandas as pd
import matplotlib.animation
import matplotlib.pyplot as plt
import sklearn.datasets
import sklearn.model_selection
import sklearn.linear_model
import sklearn.preprocessing
import sklearn.metrics
from IPython.display import HTML
1.6.3. 演習(パーセプトロン)#
sklearn.datasets のメソッドを利用して 2 クラス分類のサンプルデータを生成します。また、モデルの構築や可視化などの作業を簡単にするために、特徴量をあらかじめ平均 0 分散 1 となるように正規化します。
X, Y = sklearn.datasets.make_blobs(n_samples=200, n_features=2, centers=2, cluster_std=0.5, random_state=0)
X = sklearn.preprocessing.StandardScaler().fit_transform(X)
data = pd.concat([
pd.Series(Y, name='Y'),
pd.DataFrame(X, columns=['X1', 'X2'])
], axis='columns')
data.head()
| Y | X1 | X2 | |
|---|---|---|---|
| 0 | 1 | 1.364949 | -0.833338 |
| 1 | 1 | 0.540478 | -0.829575 |
| 2 | 1 | 1.578361 | -1.054727 |
| 3 | 1 | 0.372215 | -1.039384 |
| 4 | 0 | 0.380856 | 1.333665 |
Show code cell source
fig = plt.figure()
ax = fig.add_subplot()
ax.scatter(data['X1'][data['Y'] == 0], data['X2'][data['Y'] == 0], label='0', alpha=0.5)
ax.scatter(data['X1'][data['Y'] == 1], data['X2'][data['Y'] == 1], label='1', alpha=0.5)
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.legend()
plt.show()
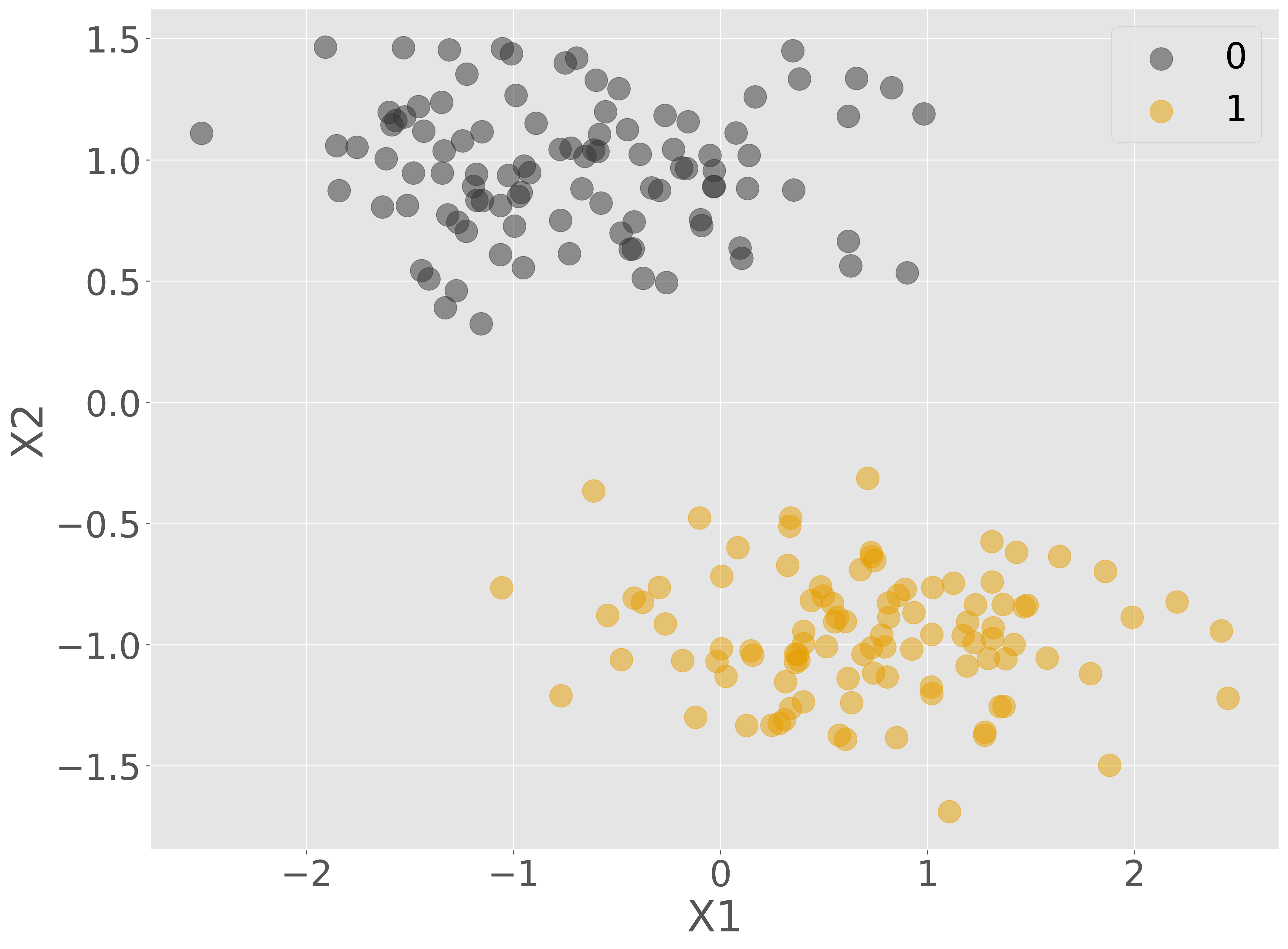
このデータを 8:2 の割合で訓練サブセットと検証サブセットに分割します。
train_data, valid_data = sklearn.model_selection.train_test_split(data, test_size=0.2, random_state=0)
次に、このサンプルデータセットにある特徴量 X1 および X2 を利用して、Y を予測するモデルを、パーセプトロンで構築します。パーセプトロンでは、
を計算し、
となるようにパラメータ \(\beta_{1}\) と \(\beta_{0}\) を推定します。パーセプトロンは、前述のように、1 サンプルずつ読み込んで、パラメータを更新しています。そこで、パーセプトロンの学習過程を見るため、プログラミング言語の繰り返し構文 for を用いて、1 ステップずつ学習させるようにし、その学習の成果をアニメーションとして出力します。
なお、パーセプトロンの学習において、パラメータに初期値として小さな値を与えて、適切な学習率を設定する必要があります。しかし、その学習過程をわかりやすく可視化するために、パラメータ(model.coef_ と model.intercept_)に大きな初期値を与えて、また、学習が遅くなるように小さな学習率(eta0)を与えています。
model = sklearn.linear_model.Perceptron(max_iter=1, eta0=0.2, warm_start=True, shuffle=True)
model.coef_ = np.array([[-100, 10]])
model.intercept_ = 10
fig = plt.figure()
ax = fig.add_subplot()
frames = ([i for i in range(101) if i % 5 == 0]) # select 1 image per 5 images for animation
ax0 = ax.scatter(train_data['X1'][train_data['Y'] == 0], train_data['X2'][train_data['Y'] == 0], label='0', alpha=0.5)
ax1 = ax.scatter(train_data['X1'][train_data['Y'] == 1], train_data['X2'][train_data['Y'] == 1], label='1', alpha=0.5)
ax_line, = ax.plot([], [], color='#0094CD', label="Decision Boundary")
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.legend()
def _update_step(i):
model.fit(train_data.drop(columns=['Y']), train_data['Y'])
w = model.coef_[0]
b = model.intercept_
if w[1] != 0:
x_vals = np.linspace(train_data['X1'].min(), train_data['X1'].max(), 100)
y_vals = -(w[0] / w[1]) * x_vals - b / w[1]
else:
x_vals = np.array([0, 0])
y_vals = np.array([train_data['X2'].min(), train_data['X2'].max()])
ax_line.set_data(x_vals, y_vals)
return ax0, ax1, ax_line
ani = matplotlib.animation.FuncAnimation(fig, _update_step, frames=frames, interval=100, repeat=False, blit=True)
html = ani.to_jshtml()
plt.close(fig)
HTML(html)

