1.7. 演習:ニューラルネットワーク#
1.7.1. ニューラルネットワーク種類#
ニューラルネットワークは、広い意味で「人工神経回路網」を指す用語であり、複数のニューロンが層状に配置されたモデル全般を指します。パーセプトロンを複数繋げて複雑な問題を解けるようにした多重パーセプトロン(multilayer perceptron; MLP)を含め、畳み込みニューラルネットワーク(convolutional neural network; CNN)、RNN(recurrent neural network; RNN)、生成敵対的ネットワーク(generative adversarial networks; GANs)などがあります。
- 多層パーセプトロン
多層パーセプトロンは、入力層から出力層の間に少なくとも 1 つの隠れ層を含み、各層のノードが完全に接続されているニューラルネットワークです。分類や回帰などに使われます。
- 畳み込みニューラルネットワーク
畳み込みニューラルネットワークは、画像の特徴(例えばエッジや形)を抽出する畳み込み層やプーリング層を組み込んだニューラルネットワークです。画像中にある物体を分類したり、検出したりするために広く使われています。
- 再帰型ニューラルネットワーク
再帰型ニューラルネットワークは、時間的に連続した情報が入力されたときに、過去の情報を記録したりするためのパラメータを持つように設計されたニューラルネットワークです。音声やテキストなどの系列データを扱うために利用されます。再帰型ニューラルネットワークを改良した長・短期記憶(long short-term memory; LSTM)やゲート付き再帰ユニット(gated recurrent unit; GRU)などもよく利用されています。
- 敵対的生成ネットワーク
敵対的生成ネットワークは、生成器と識別器という 2 つのニューラルネットワークから構成され、生成器はリアルなデータを生成しようとし、識別器はそれが本物か偽物かを判定するように、互いに競合しながら訓練するニューラルネットワークです。競合的な訓練結果、生成器は本物に近いデータが生成されるようになり、画像生成やデータ拡張などに使われています。
1.7.2. 演習準備#
本節では、次の Python ライブラリを利用します。numpy、pandas、matplotlib ライブラリはデータの読み込みや整形、可視化などに利用します。sklearn はサンプルデータセットの生成およびデータセットを訓練サブセットと検証サブセットに分けるために利用します。
import numpy as np
import pandas as pd
import matplotlib.animation
import matplotlib.pyplot as plt
import sklearn.datasets
import sklearn.model_selection
import sklearn.neural_network
import sklearn.preprocessing
import sklearn.decomposition
import sklearn.pipeline
import sklearn.metrics
from IPython.display import HTML
1.7.3. 演習(多層パーセプトロン)#
線形分離不可能なサンプルデータを生成し、多重パーセプトロンを利用して分類を行う例を示します。sklearn.datasets モジュールを利用してサンプルデータを生成し、訓練サブセットと検証サブセットに分けます。
X, Y = sklearn.datasets.make_gaussian_quantiles(n_samples=200, n_features=2, n_classes=2, random_state=0)
X = sklearn.preprocessing.StandardScaler().fit_transform(X)
data = pd.concat([
pd.Series(Y, name='Y'),
pd.DataFrame(X, columns=['X1', 'X2'])
], axis='columns')
train_data, valid_data = sklearn.model_selection.train_test_split(data, test_size=0.2, random_state=0)
data.head()
| Y | X1 | X2 | |
|---|---|---|---|
| 0 | 0 | -0.277064 | 0.144542 |
| 1 | 1 | -0.980677 | -1.466450 |
| 2 | 0 | -0.328820 | 0.362942 |
| 3 | 0 | 1.008124 | 0.332191 |
| 4 | 0 | -0.802167 | -0.606805 |
Show code cell source
fig = plt.figure()
ax = fig.add_subplot()
ax.scatter(data['X1'][data['Y'] == 0], data['X2'][data['Y'] == 0], label='0', alpha=0.5)
ax.scatter(data['X1'][data['Y'] == 1], data['X2'][data['Y'] == 1], label='1', alpha=0.5)
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.legend()
plt.show()
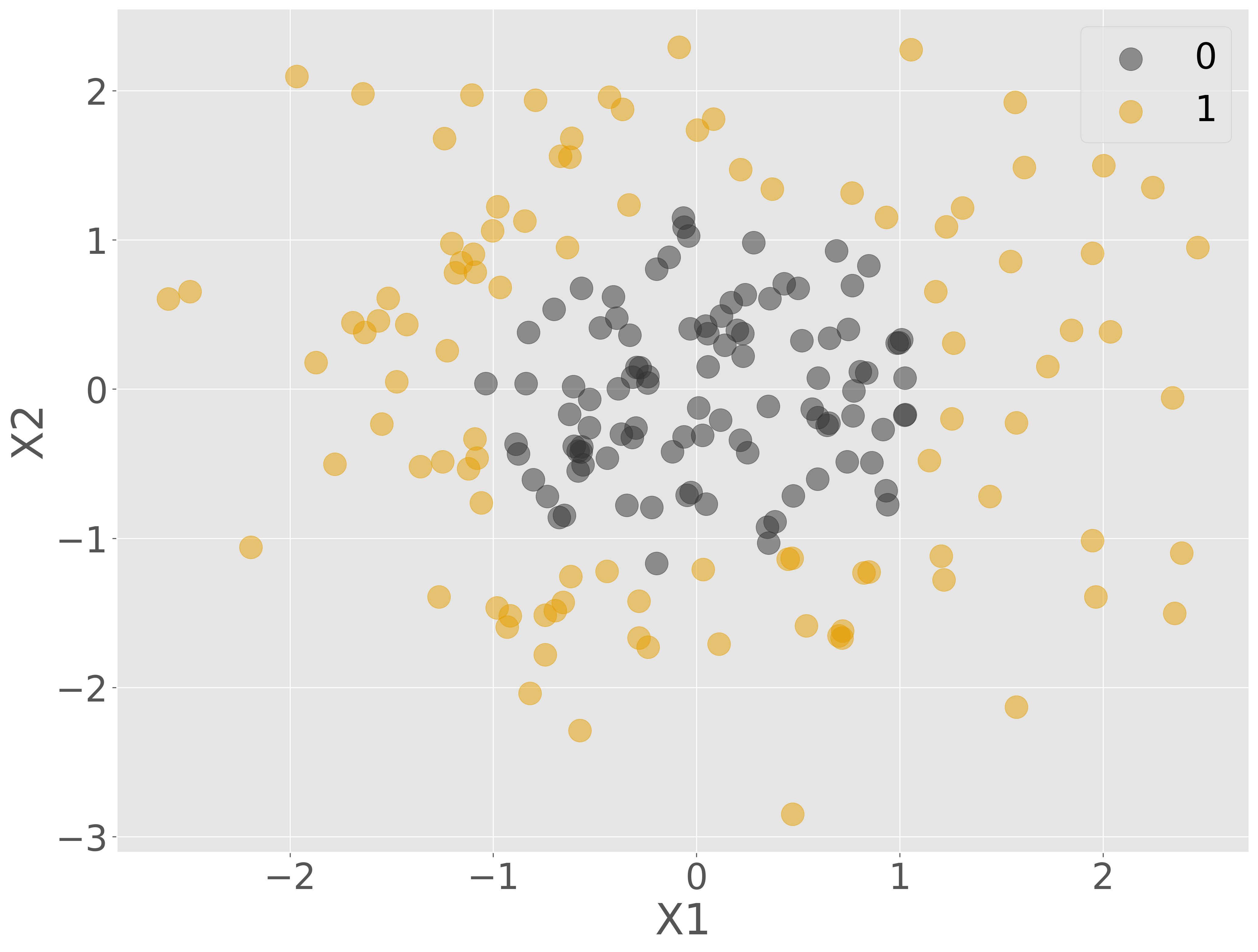
1 つのパーセプトロンは 1 本の直線を生成するため、単独では線形分離不可能なデータを分類することはできません。しかし、データの分布から、5 本の直線があればおおよそ分類できると予測されるため、パーセプトロンを 5 つ繋げたニューラルネットワークで学習効果を確認していきましょう。
Show code cell source
from graphviz import Digraph
from IPython.display import display, SVG
dot = Digraph()
dot.attr(rankdir='LR')
# input layer
dot.node('x1', 'X1', shape='circle')
dot.node('x2', 'X2', shape='circle')
# hidden layer
for i in range(1, 6):
dot.node(f'h{i}', '', shape='circle')
# output layer
dot.node('y', 'Y', shape='circle')
# connections
for input_node in ['x1', 'x2']:
for i in range(1, 6):
dot.edge(input_node, f'h{i}')
for i in range(1, 6):
dot.edge(f'h{i}', 'y')
display(SVG(dot.pipe(format='svg')))
model = sklearn.neural_network.MLPClassifier(hidden_layer_sizes=(5,), max_iter=1, learning_rate_init=0.05, warm_start=True, shuffle=True, random_state=0)
Show code cell source
model.fit(train_data.drop(columns=['Y']), train_data['Y'])
fig = plt.figure()
ax = fig.add_subplot()
frames = ([i for i in range(101) if (i + 1) % 5 == 0])
ax0 = ax.scatter(train_data['X1'][train_data['Y'] == 0], train_data['X2'][train_data['Y'] == 0], label='0', alpha=0.5, color='#333333')
ax1 = ax.scatter(train_data['X1'][train_data['Y'] == 1], train_data['X2'][train_data['Y'] == 1], label='1', alpha=0.5, color='#E69F00')
x_vals = np.linspace(train_data['X1'].min(), train_data['X1'].max(), 1000)
y_vals = np.linspace(train_data['X2'].min(), train_data['X2'].max(), 1000)
xx, yy = np.meshgrid(x_vals, y_vals)
z = model.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
contour = ax.contourf(xx, yy, z, alpha=0.3)
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.legend()
def _update_step(i):
model.fit(train_data.drop(columns=['Y']), train_data['Y'])
z = model.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
for coll in ax.collections:
coll.remove()
ax0 = ax.scatter(train_data['X1'][train_data['Y'] == 0], train_data['X2'][train_data['Y'] == 0], label='0', alpha=0.5, color='#333333')
ax1 = ax.scatter(train_data['X1'][train_data['Y'] == 1], train_data['X2'][train_data['Y'] == 1], label='1', alpha=0.5, color='#E69F00')
contour = ax.contourf(xx, yy, z, alpha=0.3)
return (ax0, ax1, contour)
ani = matplotlib.animation.FuncAnimation(fig, _update_step, frames=frames, interval=100, repeat=False, blit=False)
html = ani.to_jshtml()
plt.close(fig)
HTML(html)

