2.4. 再帰型ニューラルネットワーク

再帰型ニューラルネットワーク（recurrent neural network; RNN）は、時系列データや言語データなど、時間的な依存関係を持つデータを解析するために設計されたニューラルネットワークです。一般的なニューラルネットワークでは、データは入力層から中間層、出力層へと一方向に流れます。一方、RNN では中間層が過去の情報を記憶し、現在の入力と統合して処理する仕組みを持ちます。この設計により、RNN は連続性のあるデータを扱うのを得意としています。

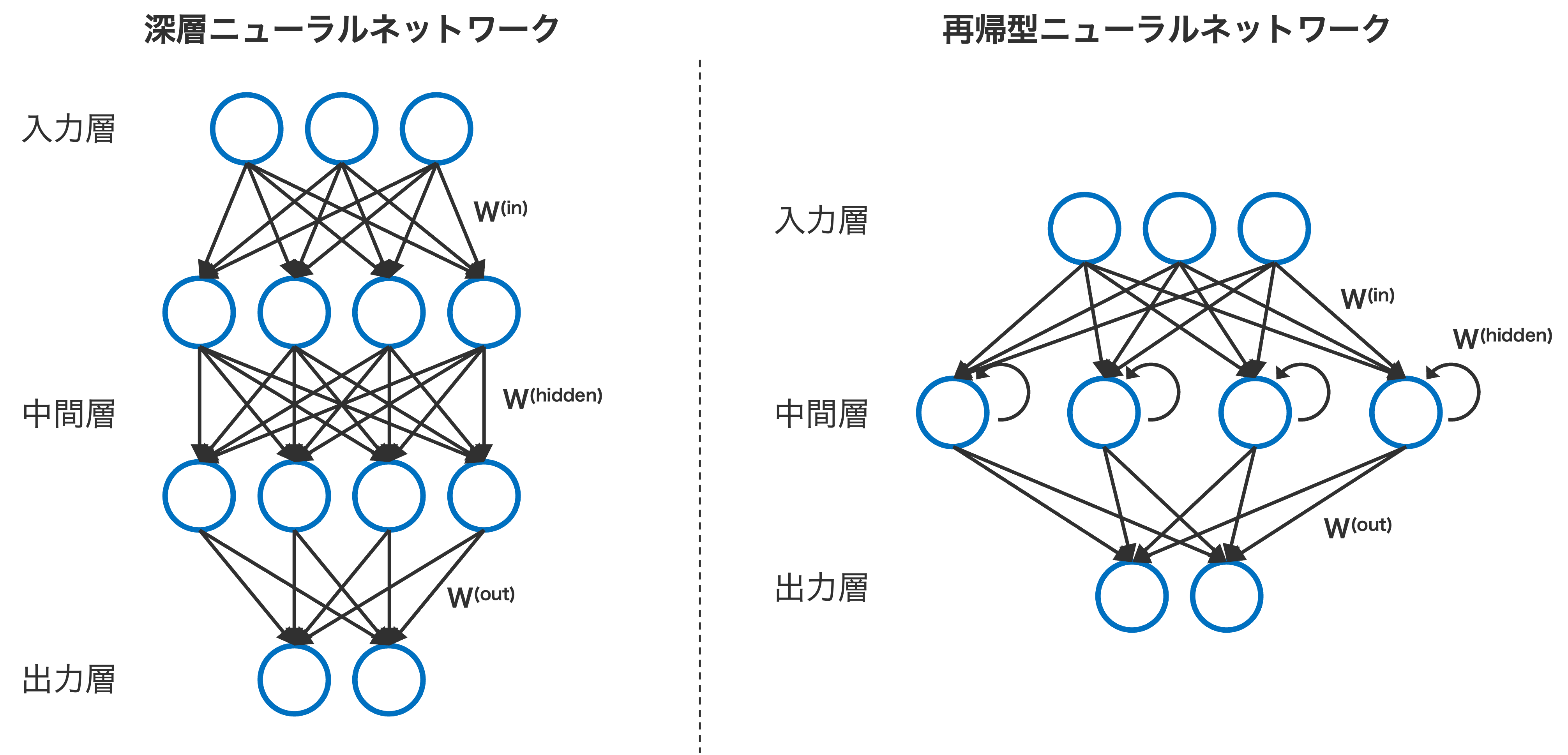
Fig. 2.1 一般的なニューラルネットワークと再帰型ニューラルネットワークのアーキテクチャの違い。

RNN の特徴的な構造は、中間層が前の時刻の出力を再利用する点です。例えば「hello world」という単語列を処理する場合、最初の時刻 (t = 1) では「h」を入力し、これを中間層が処理します。仮にその処理結果が「h’」になったとします。次の時刻 (t = 2) では、入力層から「e」を受け取ると同時に、前時刻の中間層の出力である「h’」も参照し、「h’e」を処理します。この処理結果が「h’’e’」になったとします。同様に、t = 3 では入力「l」と過去の情報「h’’e’」を統合し、「h’’e’l」処理を進めます。このように、新たな入力を受けるたびに、前の状態からの古い記録も合わせて処理できるような設計となっています。この仕組みを通じて、RNN は時間的な文脈を保持しながらデータを解析します。

RNN の利点の一つは、入力データの長さが固定されていなくても処理できる柔軟性にあります。これにより、長文の記事の要約やテキスト翻訳をはじめとして自然言語処理、音声処理、動画解析などの分野で幅広く応用されています。

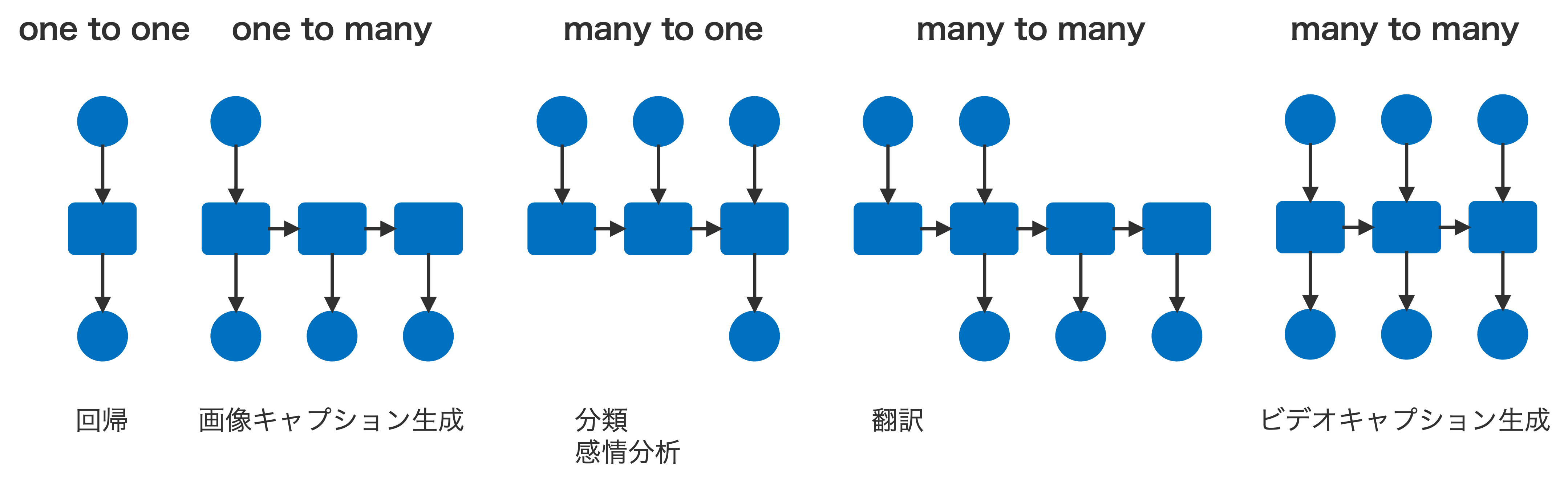
Fig. 2.2 RNN を適用できるタスクの種類。

ただし、RNN は、入力データが長くなると、古い情報が徐々に薄まるという勾配消失問題が発生しやすいことが知られています。この問題を解決するために、LSTM や GRU といった改良型ニューラルネットワークが提案されています。

2.4.1. アーキテクチャ

RNN は時系列データを処理する際に、以下のような流れで動作します。時刻または状態 \(t\) における入力を \(\mathbf{x}_t\)、中間層の隠れ状態（メモリ）を \(\mathbf{h}_t\) とします。この隠れ状態 \(\mathbf{h}_t\) は、その時刻の入力データ \(\mathbf{x}_t\) と前の時刻の隠れ状態 \(\mathbf{h}_{t-1}\) を統合して計算されます。具体的には、入力 \(\mathbf{x}_t\) に対して重み \(\mathbf{U}\) を、前の隠れ状態 \(\mathbf{h}_{t-1}\) に対して重み \(\mathbf{V}\) を掛け合わせ、次に、バイアス項 \(\mathbf{b}_h\) を加えます。

\[ \mathbf{z}_{t} = \mathbf{U}\mathbf{x}_t + \mathbf{V}\mathbf{h}_{t-1} + \mathbf{b}_h \]

次に、これらの和を活性化関数 \(\phi\) に代入して、隠れ状態 \(\mathbf{h}_t\) を計算します。通常、\(\tanh\) や \(\text{ReLU}\) などの非線形関数が活性化関数として使用されます。

\[ \mathbf{h}_t = \phi \left( \mathbf{z}_{t} \right) \]

隠れ状態 \(\mathbf{h}_t\) は、その時刻の入力情報と過去の情報を統合した特徴表現を表します。次に、RNN の出力 \(\mathbf{y}_t\) は、この隠れ状態 \(\mathbf{h}_t\) に基づいて計算されます。具体的には、隠れ状態 \(\mathbf{h}_t\) に重み行列 \(\mathbf{W}\) を掛け、その結果にバイアス項 \(\mathbf{b}_y\) を加えたものをさらに活性化関数 \(\phi\) に代入します。

\[ y_t = \phi \left( \mathbf{W}\mathbf{h}_t + \mathbf{b}_y \right) \]

RNN は、1 つの入力に対して 1 つの出力 \(y_t\) を逐次生成します。たとえば、言語データを入力した場合、入力された文字の数だけ対応する出力が得られます。これらの出力は、タスクの目的に応じて柔軟に利用されます。たとえば、言語生成や時系列予測のように、各時刻におけるすべての出力 \(y_t (t = 1, 2, \cdots)\) を必要とするタスクでは、それぞれの \(y_t\) を活用します。一方で、文章全体の感情分類など、全体的な情報が求められるタスクでは、最後の時刻に得られる出力 \(y_T\) のみを用いることが一般的です。

2.4.2. RNN の学習

RNN の学習には損失関数が必要です。まず、時刻 \(t\) における予測値 \(\hat{y}_t\) と実際の測定値 \( y_t\) の誤差を定義し、その誤差を全ての時刻にわたって合計して損失 \(J\) を計算します。予測値と測定値の誤差を測る指標は、タスクの目的に応じて異なります。例えば、回帰問題の場合は RMSE（Root Mean Square Error）を使用し、分類問題の場合は交差エントロピー損失を使用します。

\[ J = \sum_{t} \left( y_t - \hat{y}_t \right)^2 \]

RNN では、誤差逆伝播法（backpropagation）を時系列データに拡張した backpropagation through time（BPTT）と呼ばれる手法を用いて学習を行います。BPTT では、各時刻の誤差を計算し、それをネットワーク上で逆伝播させていきます。これにより、RNN のパラメータ（\( \mathbf{U}, \mathbf{V}, \mathbf{W} \)）とバイアス項（\( \mathbf{b}_h, \mathbf{b}_y \)）を最適化していきます。

BPTT では、誤差が時間をさかのぼって伝播されるため、各時刻におけるパラメータ更新が行われます。しかし、長い時系列の場合、勾配消失や勾配爆発が発生することがあるため、その対策として LSTM や GRU などの改良型 RNN が利用されることが多いです。

2.4.3. 双方向性再帰型ニューラルネットワーク

双方向性再帰型ニューラルネットワーク（bidirectional RNN）は、入力データが過去の情報だけでなく、未来の情報も考慮して処理を行うネットワークです。通常の RNN は、データを時系列順に処理しますが、双方向性 RNN では、過去から未来への順伝播と未来から過去への逆伝播の両方向で情報を伝播させます。このため、学習時には過去と未来の両方の入力データが必要となります。しかし、運用時には、ある時刻 \(t\) の出力 \(y_t\) を得るために前後の情報が必要となるため、その適用範囲が制限される場合があります。例えば、文章全体が入力されてから翻訳が行われるタスク（機械翻訳など）には有効です。しかし、話し手がまだ言葉を言い終わっていない段階で通訳を進める必要がある逐次通訳のようなケースでは、双方向性 RNN を利用することはできません。

双方向性 RNN の順伝播では、時刻 \( t \) における中間層の計算が行われます。順伝播では、現在の入力 \(\mathbf{x}_t\) と、1つ前の時刻の隠れ層状態 \( \mathbf{z}_{t-1}\) を使って、次の中間層の状態 \(\overrightarrow{\mathbf{z}}_t \) を計算します。その後、この状態に活性化関数 \( \phi \) を適用して、順伝播の隠れ層出力 \( \overrightarrow{\mathbf{H}}_t \) を得ます。

\[ \overrightarrow{\mathbf{z}}_{t} = \mathbf{U}^{(f)} \mathbf{x}_t + \mathbf{V}^{(f)} \mathbf{z}_{t-1} + \mathbf{b}_z^{(f)} \]

\[ \overrightarrow{\mathbf{H}}_{t} = \phi \left( \overrightarrow{\mathbf{z}}_t \right) \]

逆伝播では、未来の情報を考慮して計算を行います。時刻 \( t \) の中間層は、現在の入力 \( \mathbf{x}_t \) と、次の時刻 \( t+1 \) の隠れ層状態 \( \mathbf{z}_{t+1} \) を使って、逆伝播の中間層の状態 \( \overleftarrow{\mathbf{z}}_t \) を計算します。その後、活性化関数 \( \phi \) を適用して、逆伝播の隠れ層出力 \( \overleftarrow{\mathbf{H}}_t \) を得ます。

\[ \overleftarrow{\mathbf{z}}_{t} = \mathbf{U}^{(b)} \mathbf{x}_t + \mathbf{V}^{(b)} \mathbf{z}_{t+1} + \mathbf{b}_z^{(b)} \]

\[ \overleftarrow{\mathbf{H}}_{t} = \phi \left( \overleftarrow{\mathbf{z}}_t \right) \]

順伝播と逆伝播の隠れ層状態が計算されると、次にこれらを組み合わせて出力値を計算します。具体的には、順伝播の隠れ層出力と逆伝播の隠れ層出力を縦に結合して、1 つのベクトルを作成します。次に、このベクトルに重み行列 \(\mathbf{W}\) を掛け、バイアス項 \(\mathbf{b}_y\) を加え、活性化関数 \(\phi\) を適用して、最終的な出力 \(y_t\) を計算します。

\[\begin{split} y_t = \phi \left( \begin{pmatrix} \overrightarrow{\mathbf{H}}_t \\ \overleftarrow{\mathbf{H}}_t \end{pmatrix} \mathbf{W} + \mathbf{b}_y \right) \end{split}\]

この出力は、RNN と同様に予測値と実際の値との差を損失関数として定義し、学習を行う際に最適なパラメータを求めます。

このように、双方向性RNNは、未来と過去の両方向から情報を取り込むことによって、文脈の理解に優れた性能を発揮します。しかし、運用時には未来の情報が必要となるため、将来の予測タスクには適さない場合があります。