長・短期記憶

2.5. 長・短期記憶#

長・短期記憶（long short-term memory; LSTM）は、長期記憶を効率的に扱うために設計された再帰型ニューラルネットワークの一種です。通常の RNN は、勾配を逆伝播することで学習を行いますが、時刻が長くなると、勾配が消失したり発散したりする問題が発生します。この現象により、長期的な依存関係を持つデータに対して、適切に学習を行うことが難しくなります。この問題を解決するために提案されたのが LSTM です。LSTMでは、内部に記憶セルが組み込まれており、このセルは情報を長期間に保持することができます。記憶セルは、新しい情報を加えたり、古い情報を削除したりすることができ、これにより適切な長期記憶が可能になります。LSTM は翻訳、音声認識、キャプション生成など、さまざまな分野で広く利用されています。

2.5.1. アーキテクチャ#

通常の RNN では、データは入力層、中間層、出力層の順に伝播され、その結果が出力されます。LSTM も基本的には同じ仕組みで、データは入力層、中間層、出力層の順に伝播されます。しかし、RNN の中間層は 1 つの活性化関数を使用するのに対して、LSTM の中間層では複数の活性化関数が使用され、複雑な演算が行われます。この LSTM の中間層のことをセルまたは LSTM ブロックと呼びます。LSTM ブロックでの複雑な演算が、LSTM の特徴であり、長期的な依存関係を保持するための重要な要素となっています。

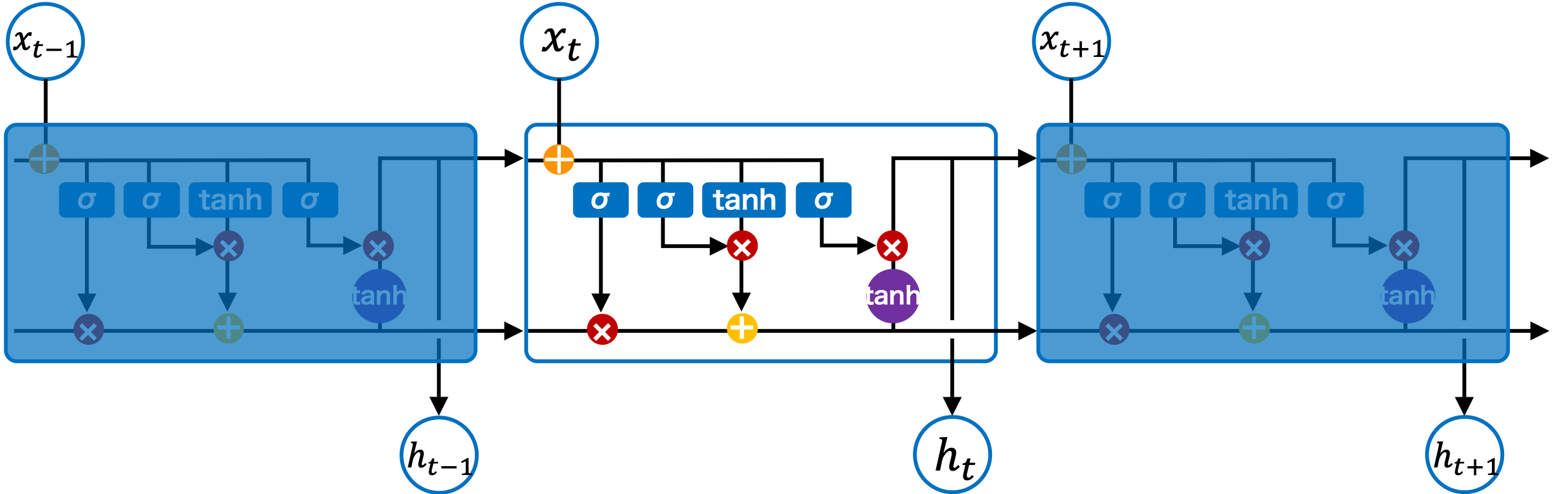
../_images/lstm-block-arch.png — Fig. 2.3 LSTM ブロックのアーキテクチャ。#

2.5.1.1. 長期記憶#

LSTM では、LSTM ブロック内に長期記憶を保持するための変数 \(\mathbf{C}_t\) が用意されています。この長期記憶に対して、古くなった情報を削除したり、新しい情報を追加したりすることで、適切な長期記憶を維持します。具体的には、前の状態から伝達された長期記憶 \(\mathbf{C}_{t-1}\) に対して、\(0\) から \(1\) の間で決まる割合（忘却率）を掛け合わせ、古い記憶をどれくらい忘れるかを調整します。その後、入力と現在の状態から得られた新しい情報を長期記憶に追加し、次の状態に伝達します。

../_images/lstm-block-longmemory.png — Fig. 2.4 LSTM ブロックの長期記録を制御するモジュール。#

2.5.1.2. 忘却ゲート#

LSTM の忘却ゲート（forget gate）は、長期記憶から情報を「忘れる」ための制御を行います。入力 \(\mathbf{x}_t\) と 1 つ前のセルの隠れ状態 \(\mathbf{h}_{t-1}\) を基に、忘却率 \(\mathbf{f}_t\) を計算します。この忘却率はシグモイド関数で計算され、各要素が \(0\) 以上 \(1\) 以下の値を取ります。

\[ \mathbf{f}_t = \sigma \left( \mathbf{W}_f \mathbf{x}_t + \mathbf{U}_f \mathbf{h}_{t-1} + \mathbf{b}_f \right) \]

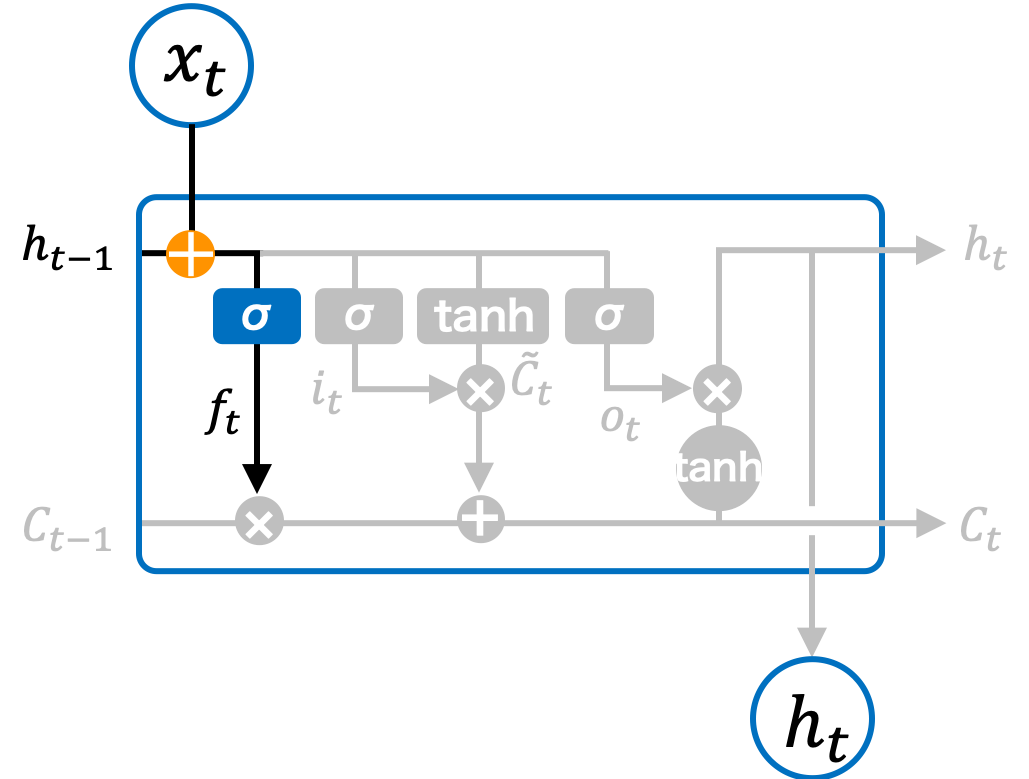
../_images/lstm-block-forgetgate.png — Fig. 2.5 LSTM ブロックの忘却ゲート。#

\(\mathbf{f}_t\) は、1 つ前のセルの長期記憶 \(\mathbf{C}_{t-1}\) に掛け算され、どの程度記憶を維持するかを決定します。正しくはないが、わかりやすく例えるならば、ある要素 \(\mathbf{C}_j\) に対して \(\mathbf{f}_j = 1.0\) であれば、その記憶は保持され、\(\mathbf{f}_j = 0.2\) であれば、その記憶は 80% 忘れられます。

2.5.1.3. 入力ゲート#

次に、入力ゲート（input gate）では、入力 \(\mathbf{x}_t\) と 1 つ前のセルの隠れ状態 \(\mathbf{h}_{t-1}\) を基に、現在のセルの状態候補 \(\tilde{\mathbf{C}}_t\) を計算します。この値が、新たに長期記憶に追加する情報となります。

\[ \tilde{\mathbf{C}}_t = \tanh \left( \mathbf{W}_C \mathbf{x}_t + \mathbf{U}_C \mathbf{h}_{t-1} + \mathbf{b}_C \right) \]

ただし、\(\tilde{\mathbf{C}}_t\) の全ての情報を長期記憶に保存するわけではなく、必要な情報だけを保存する方が効率的です。そのため、\(\tilde{\mathbf{C}}_t\) に記憶率 \(\mathbf{i}_t\) を掛けて、必要な情報を選別します。この記憶率 \(\mathbf{i}_t\) もシグモイド関数によって計算され、各要素は \(0\) 以上 \(1\) 以下の値を取ります。

\[ \mathbf{i}_t = \sigma \left( \mathbf{W}_i \mathbf{x}_t + \mathbf{U}_i \mathbf{h}_{t-1} + \mathbf{b}_i \right) \]

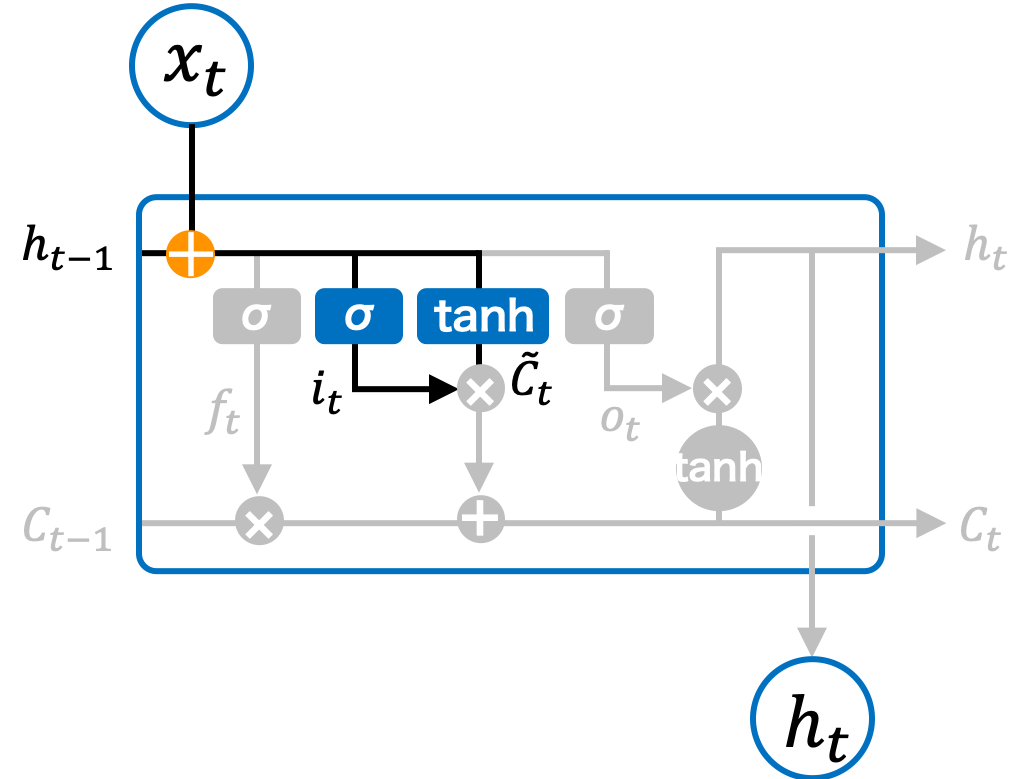
../_images/lstm-block-inputgate.png — Fig. 2.6 LSTM ブロックの入力ゲート。#

2.5.1.4. 長期記憶の更新#

長期記憶 \(\mathbf{C}_t\) は、1 つ前のセルの長期記憶 \(\mathbf{C}_{t-1}\) に対して、忘却率を掛けて不要な情報を削除し、さらに新たに計算された情報を追加して更新されます。この更新は以下の式で表されます。ここで、\(\odot\) はアダマール積（成分ごとの積）を示します。

\[ \mathbf{C}_t = \mathbf{f}_t \odot \mathbf{C}_{t-1} + \mathbf{i}_t \odot \tilde{\mathbf{C}}_t \]

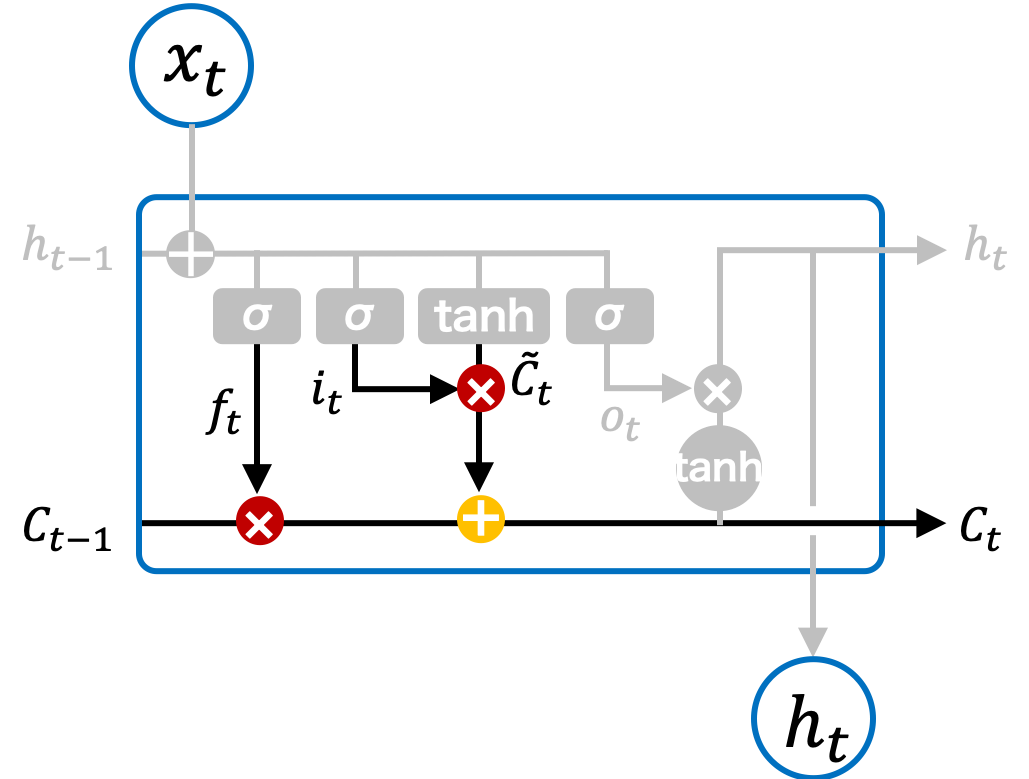
../_images/lstm-block-longmemory-update.png — Fig. 2.7 LSTM ブロックの長期記憶を更新するモジュール。#

2.5.1.5. 出力ゲート#

最終的に、状態 \(t\) のセルの出力は、入力 \(\mathbf{x}_t\) と前の隠れ状態 \(\mathbf{h}_{t-1}\) を基に、現在の長期記憶を使用して計算されます。出力ゲート \(\mathbf{o}_t\) は、現在の入力と前の隠れ状態を基に計算され、これを用いて長期記憶 \(\mathbf{C}_t\) を処理した後、最終的な隠れ状態 \(\mathbf{h}_t\) が得られます。

\[ \mathbf{o}_t = \sigma \left( \mathbf{W}_o \mathbf{x}_t + \mathbf{U}_o \mathbf{h}_{t-1} + \mathbf{b}_o \right) \]

\[ \mathbf{h}_t = \mathbf{o}_t \odot \tanh(\mathbf{C}_t) \]

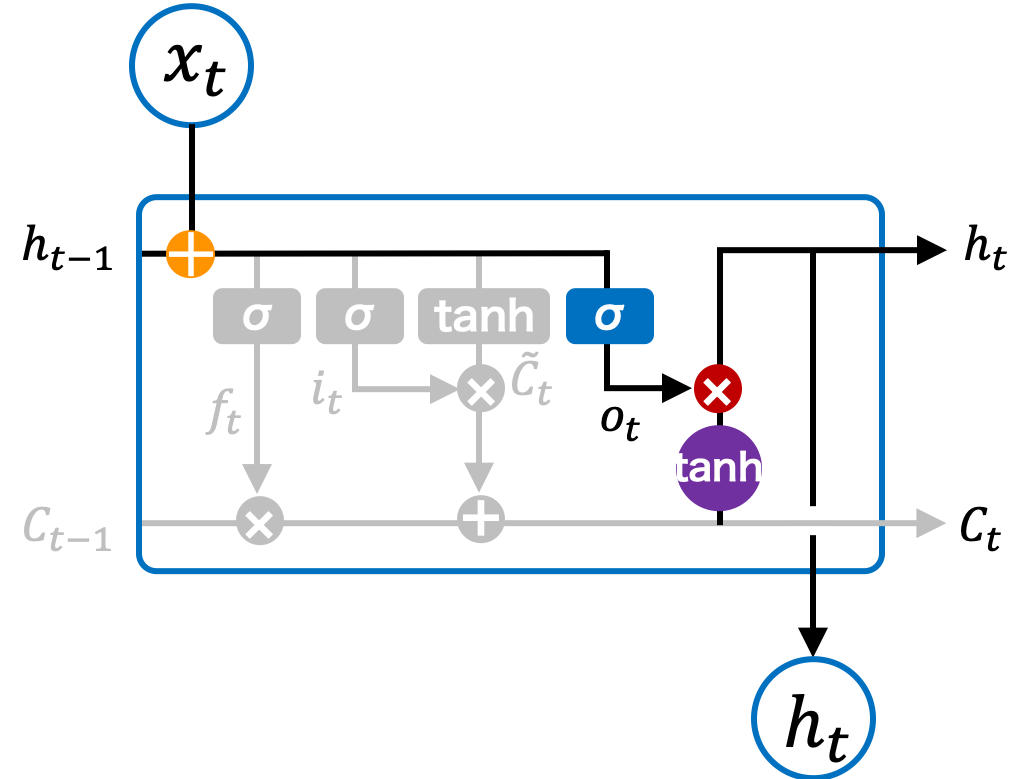
../_images/lstm-block-outputgate.png — Fig. 2.8 LSTM ブロックの出力ゲート。#

このように、LSTMでは忘却、入力、出力の各ゲートを使って、必要な情報を効率的に保持し、伝播させながら学習を行います。

2.5.2. 双方向性長・短期記憶#

LSTM（長・短期記憶）は、現在の状態の中間層の出力を次の状態に順伝播させるネットワークです。一方、双方向性長・短期記憶（Bidirectional LSTM; BLSTM）は、LSTM の出力を未来への順伝播と過去への逆伝播の両方向で伝播させるネットワークです。この双方向性により、BLSTM は未来の情報も過去の情報も同時に利用できるため、特に文脈依存が強いタスクにおいて有利です。

BLSTM は、BRNN（Bidirectional RNN）と同じく、過去と未来の両方の情報を入力として利用しますが、LSTM セルを使うことで、長期記憶の保持に優れ、より強力なモデルとなります。そのため、BRNN と比較して、長期依存性を扱うタスクでの性能が向上します。しかし、BLSTM も BRNN と同様に、予測のためには過去と未来の情報両方を必要とするため、リアルタイム予測などの応用には制約がある点に注意が必要です。